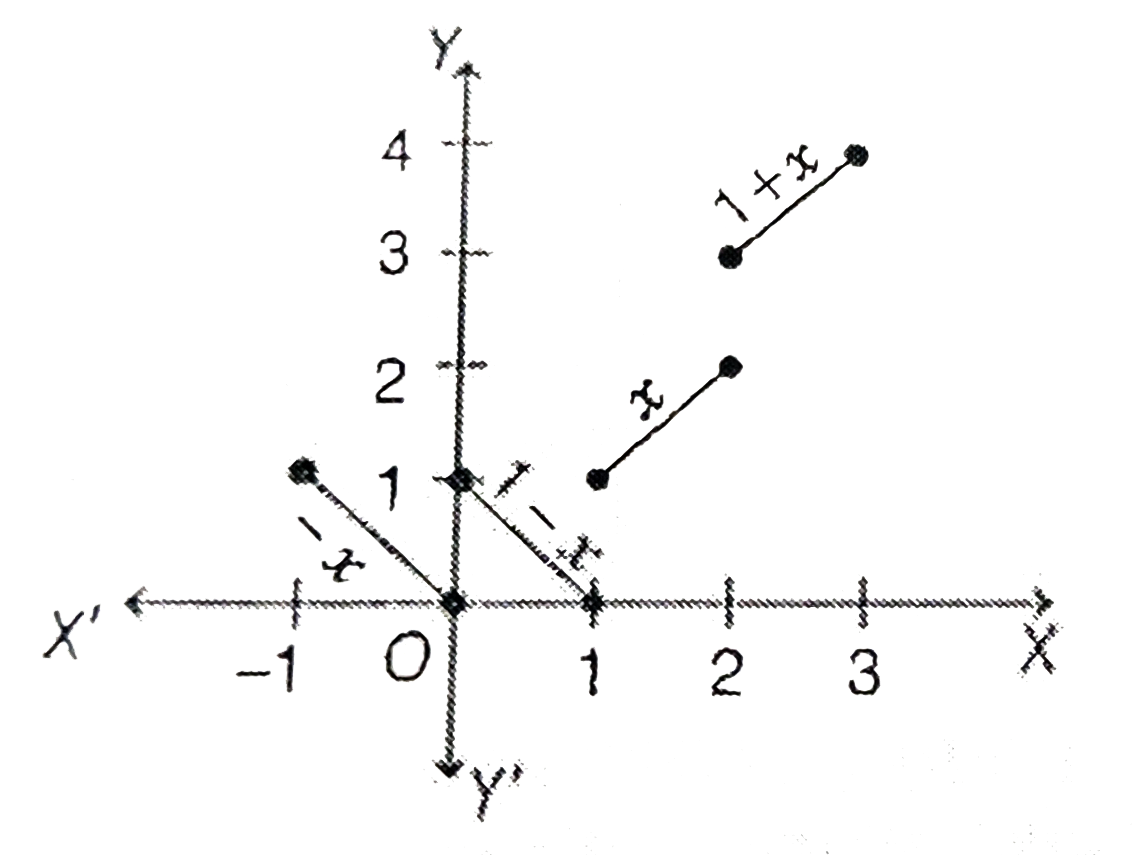
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Draw a graph of the function y = [x] +|1 - x|,-1 leq x leq 3. Determi...
Text Solution
|
- Let f(x)=f1(x) where where f1(x) ={min{x^2,|x|}, |x| leq 1 max {x^...
Text Solution
|
- Draw a graph of the function y=[x]+|1-x|,-1<=x<=3. Determine the point...
Text Solution
|
- If function defined by f(x) ={(x-m)/(|x-m|) , x leq 0 and 2x^2+3ax+b ...
Text Solution
|
- If f: x: -1 leq x leq 1 -> {x : -1 leq x leq 1} , then which is/are bi...
Text Solution
|
- Let f(x)=min{x-[x|,-[-x)],-2lt=xlt=2,g(x)=|2-|x-2||,-2lt=xlt=2 and h(x...
Text Solution
|
- Let f:[1,3]->R be a function satisfying x/([x]) leq f(x) leq sqrt(6-x)...
Text Solution
|
- फलन y=|x|+|x-1| का ग्राफ खींचिए ।
Text Solution
|
- Draw the graph of the function y=|x-1|+|x+1| and examine whether f(x) ...
Text Solution
|