Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
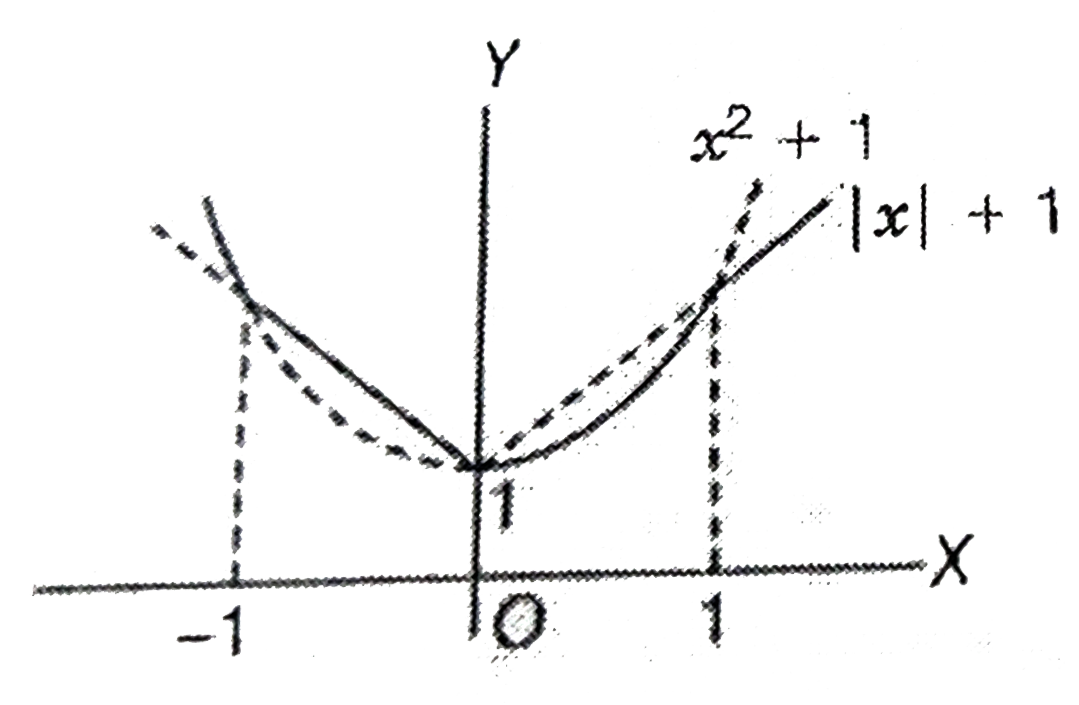
- Let f : R to R and g: R to R be , respectively, given by f(x) = |x|+1...
Text Solution
|
- Consider f g and h are real-valued functions defined on R. Let f(x)-f(...
Text Solution
|
- Let f:R rarr R and g:R rarr R be respectively given by f(x)=|x|+1 and ...
Text Solution
|
- Let f:R to R and h:R to R be differentiable functions such that f(x)=x...
Text Solution
|
- If f: R to R, g , R to R be two funcitons, and h(x) = 2 "min" {f(x) - ...
Text Solution
|
- If f : R to R and g : R to R are given by f(x)=|X| and g(x)=[x] for ea...
Text Solution
|
- माना f: R to R, g : R to R व h: R to R तीन फलन इस प्रकार है की f(x)=x^...
Text Solution
|
- Let f, g: R to R by f(x) = x|x| -1 AA x in R and g(x) = {{:(3/2x, if...
Text Solution
|
- Let f:R to R and h:R to R be differentiable functions such that f(x)=x...
Text Solution
|