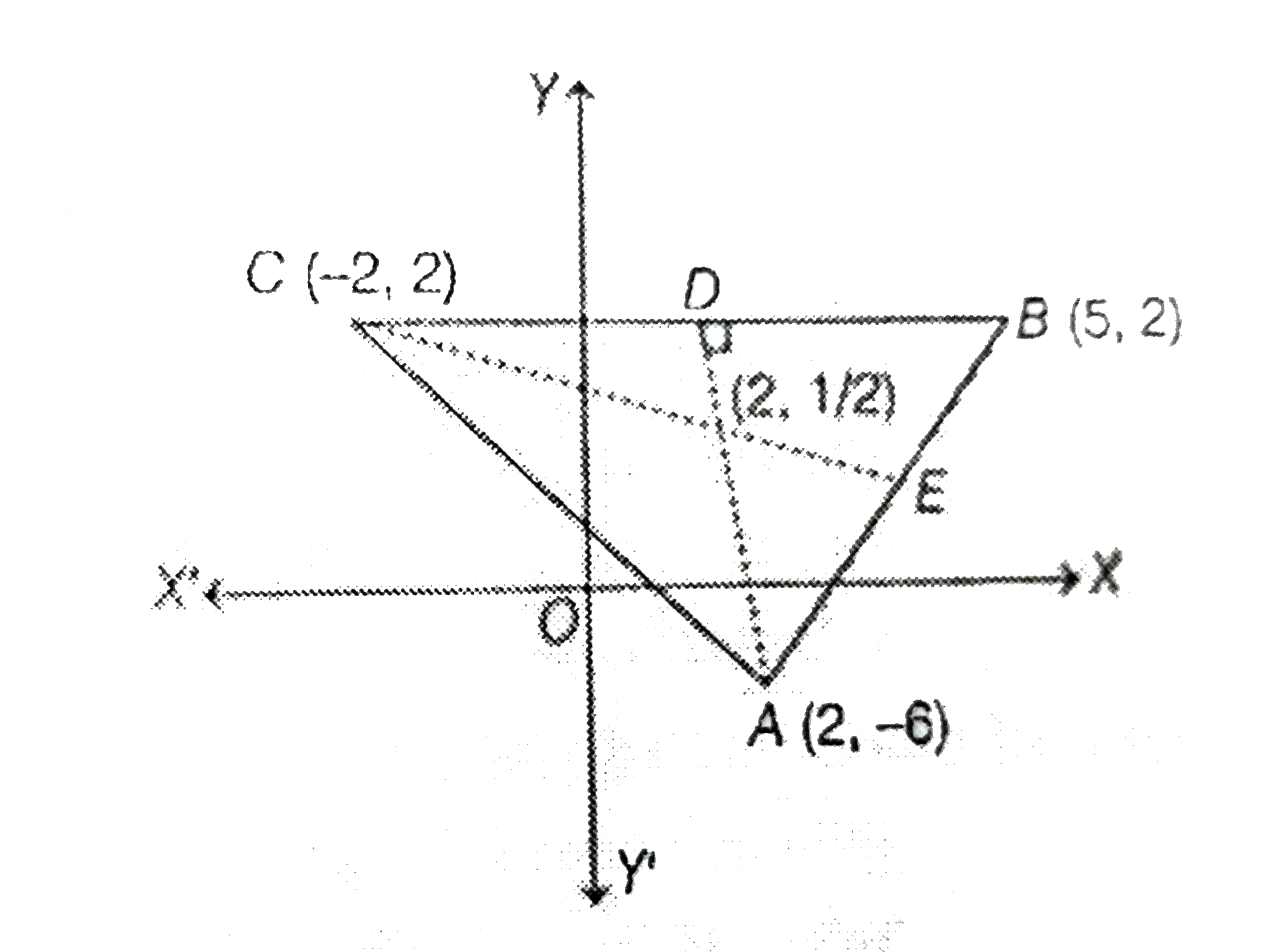
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let k be in integer such that triangle with vertices (k,-3k),(5,k) an...
Text Solution
|
- Let k be an integer such that the triangle with vertices (k ,-3k),(...
Text Solution
|
- Let k be an integer such that the triangle with vertices (k, -3k), (5,...
Text Solution
|
- माना k एक ऐसा पूर्णाक है कि त्रिभुज, जिसके शीर्ष (k,-3k),(5,k) तथा (-...
Text Solution
|
- মনে করো k একটি পূর্ণসংখ্যা। যদি (k, -3k), (5, k) এবং (-k, 2) বিন্দুত্র...
Text Solution
|
- Find the values of k so that the area of the triangle with vertices (1...
Text Solution
|
- माना k एक ऐसा पूर्णांक हैं कि त्रिभुज, जिसके शीर्ष (k, - 3k) , (5,k) ...
Text Solution
|
- Find the values of k so that the area of the triangle with vertices (1...
Text Solution
|
- Let k be an integer such that the triangle with vertices (k ,-3k),(5...
Text Solution
|