A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
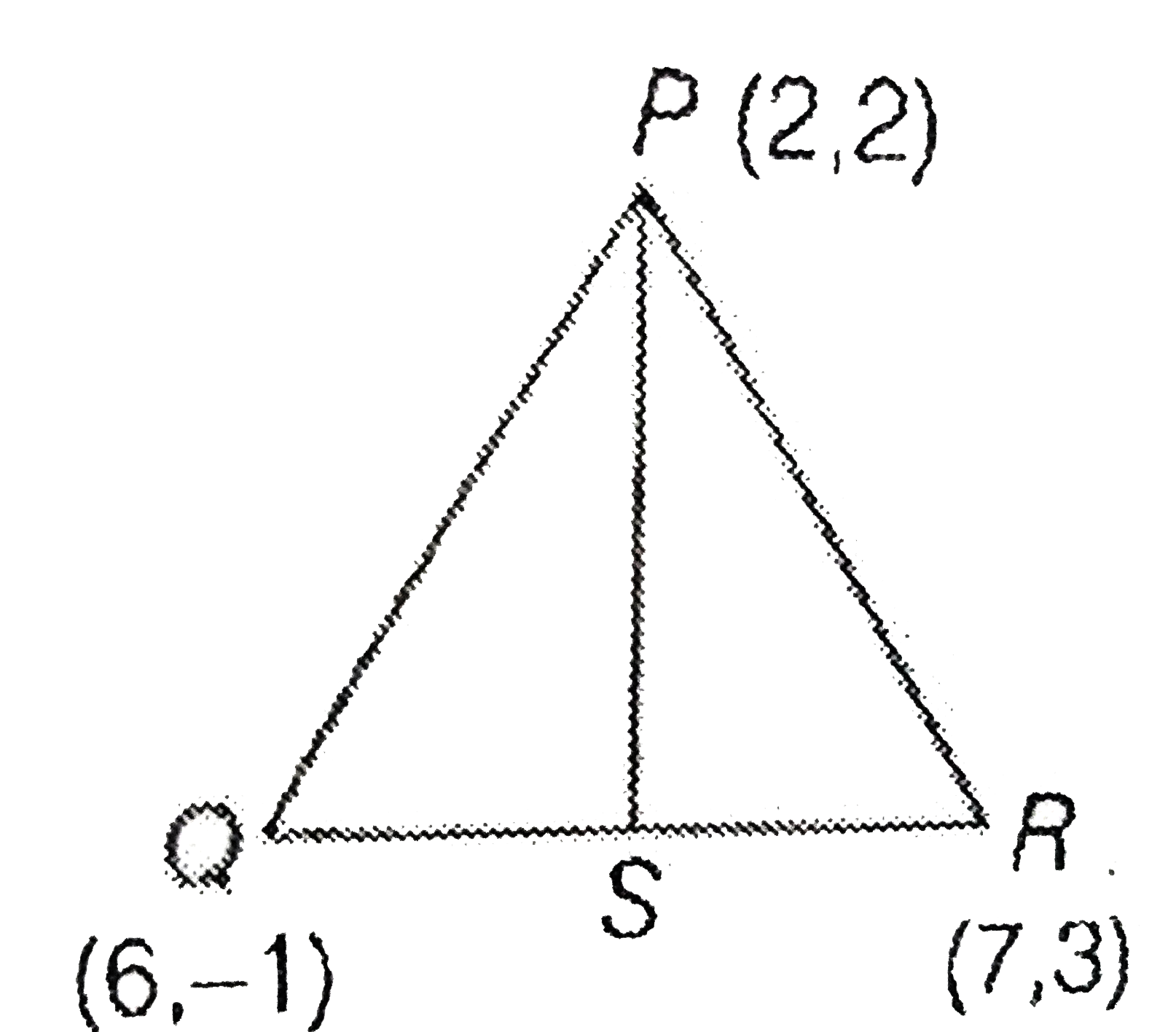
- Let PS be the median of the triangle with vertices P(2, 2), Q(6, -1) a...
Text Solution
|
- Let PS be the median of the triangle with vertices P(2,""2),""Q(6,-1)"...
Text Solution
|
- Let PS be the median of the triangle with vertices P(2,2),Q(6,-1) and ...
Text Solution
|
- Let PS be the median of the triangle with vertices P (2 ,2) , Q (6 , -...
Text Solution
|
- Let PS be the median of the triangle with vertices P(2,2),Q(6,-1) and...
Text Solution
|
- If PS is the median of the triangle with vertices P(2, 2), Q(6, –1) a...
Text Solution
|
- Let PS be the median of the triangle with vertices P(2, 2), Q(6, -1) a...
Text Solution
|
- त्रिभुज, जिसके शीर्ष P(2,2),Q(6, - 1) व R(7,3) हैं, की माध्यिका PS है।...
Text Solution
|
- माना PS एक त्रिभुज की माध्यिका है, जिसके शीर्ष P(2, 2), Q(6, -1) ...
Text Solution
|