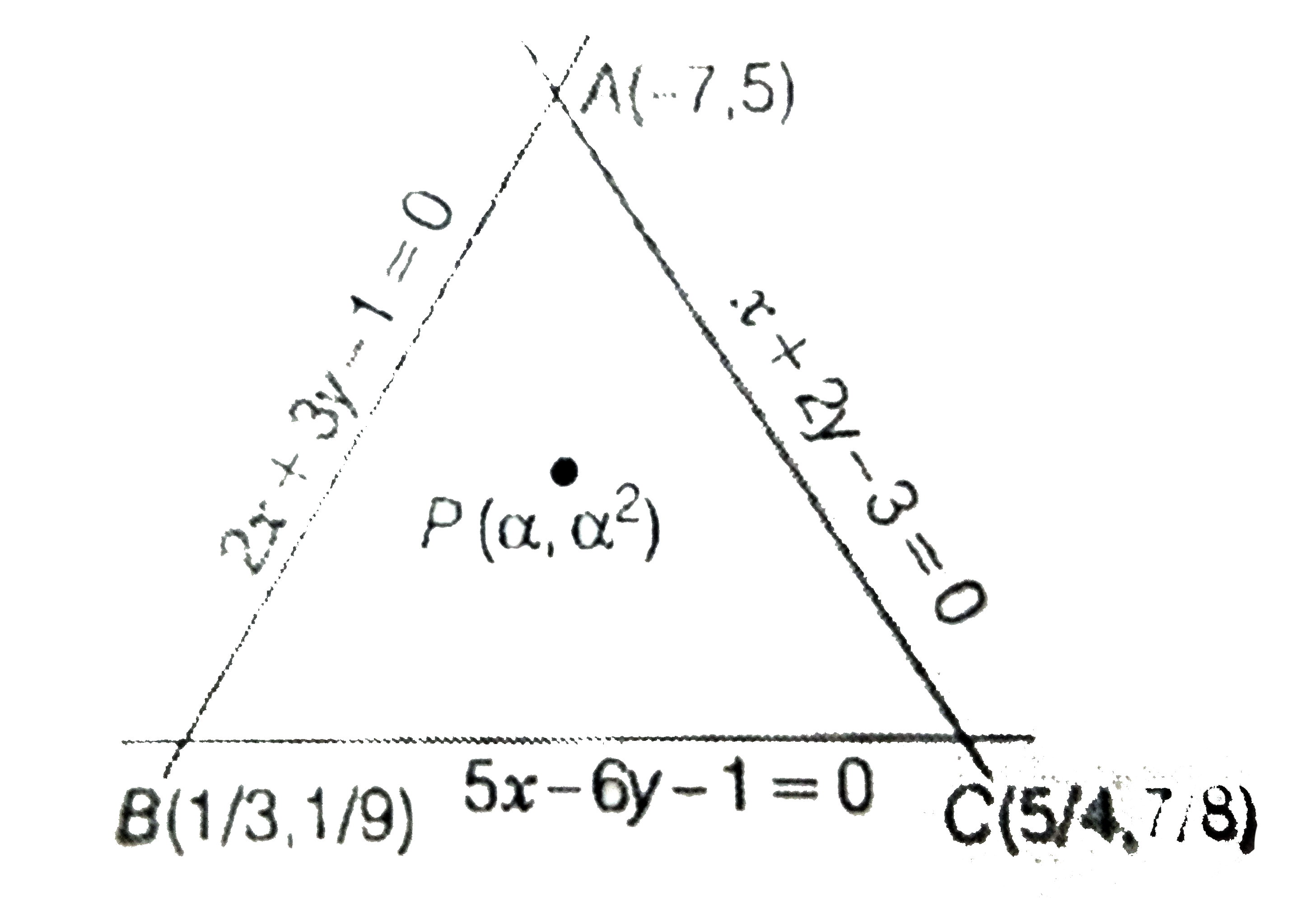Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Determine all the values of alpha for which the point (alpha,alpha^2) ...
Text Solution
|
- Find the values of alpha so that the point P(alpha^2,alpha) lies insid...
Text Solution
|
- Determine all the values of alpha for which the point (alpha,alpha^2) ...
Text Solution
|
- The range of value of alpha such that (0,alpha) lies on or inside the ...
Text Solution
|
- Detemine all values of alpha for which the point (alpha, alpha^(2)) li...
Text Solution
|
- alpha के वे सभी मान ज्ञात कीजिए जिनके लिए बिन्दु (alpha, alpha^(2)) त...
Text Solution
|
- Consider the Delta formed by the lines y+3x+2=0,3y-2x-5=0,4y =0 The po...
Text Solution
|
- Determine all the values of alpha for which the point (alpha,alpha^2) ...
Text Solution
|
- Determine all the values of alpha for which the point (alpha,alpha^2) ...
Text Solution
|