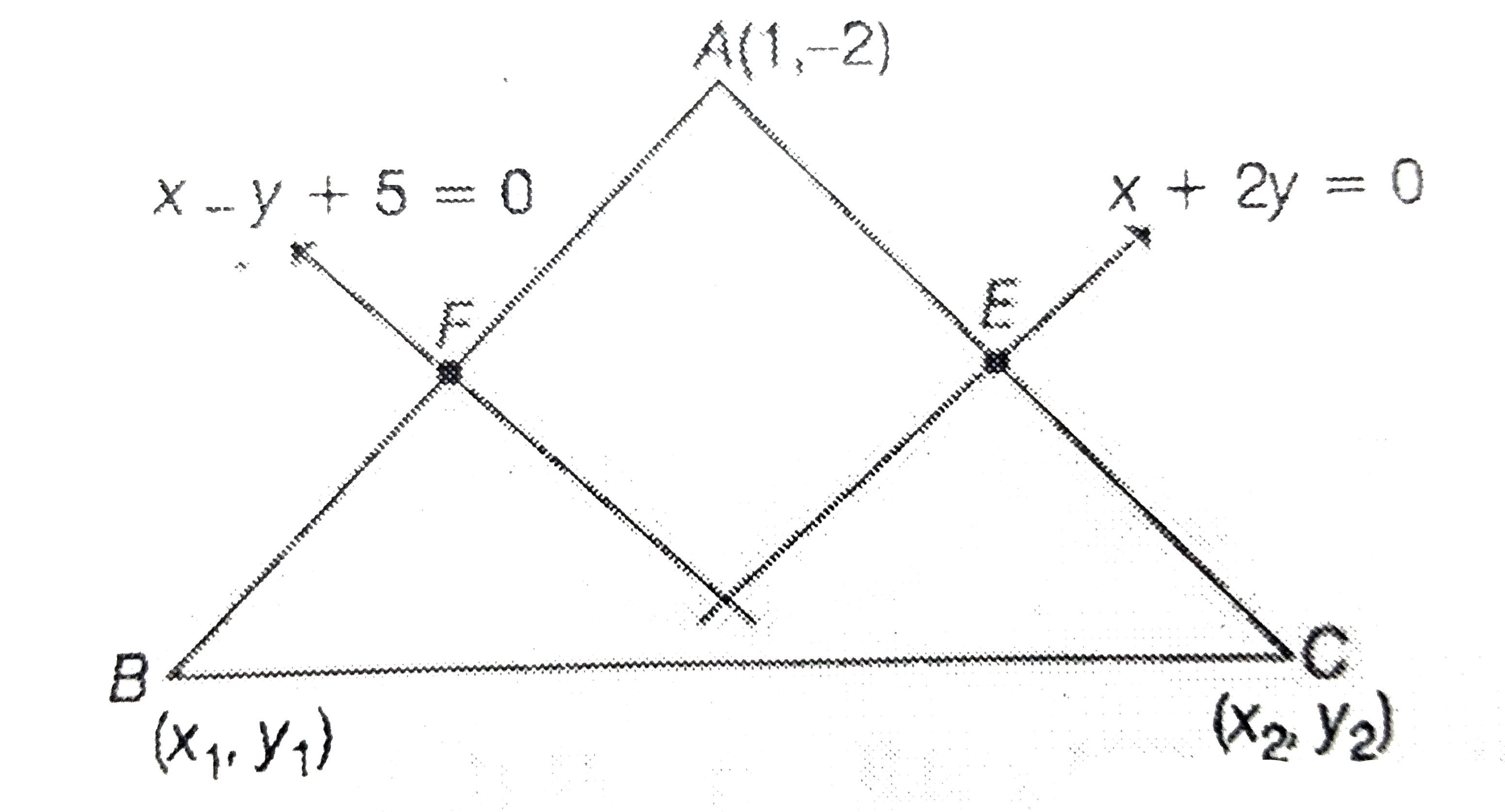Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The equations of the perpendicular bisectors of the sides A Ba n dA C ...
Text Solution
|
- The equations of the perpendicular bisectors of the sides A Ba n dA C ...
Text Solution
|
- the equation of perpendicular bisectors of side AB,BC of triangle ABC ...
Text Solution
|
- The equations of the perpendicular bisector of the sides AB and perpen...
Text Solution
|
- The equations of the perpendicular bisectors of the sides AB and AC of...
Text Solution
|
- If the equations of the perpendicular bisectors of the sides AB and AC...
Text Solution
|
- If the equations of the perpendicular bisectors of the sides Ab and AC...
Text Solution
|
- The equation of perpendicular bisectors of AB and AC of a triangle ABC...
Text Solution
|
- In triangle A B C , the equation of the right bisectors of the sides A...
Text Solution
|