Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
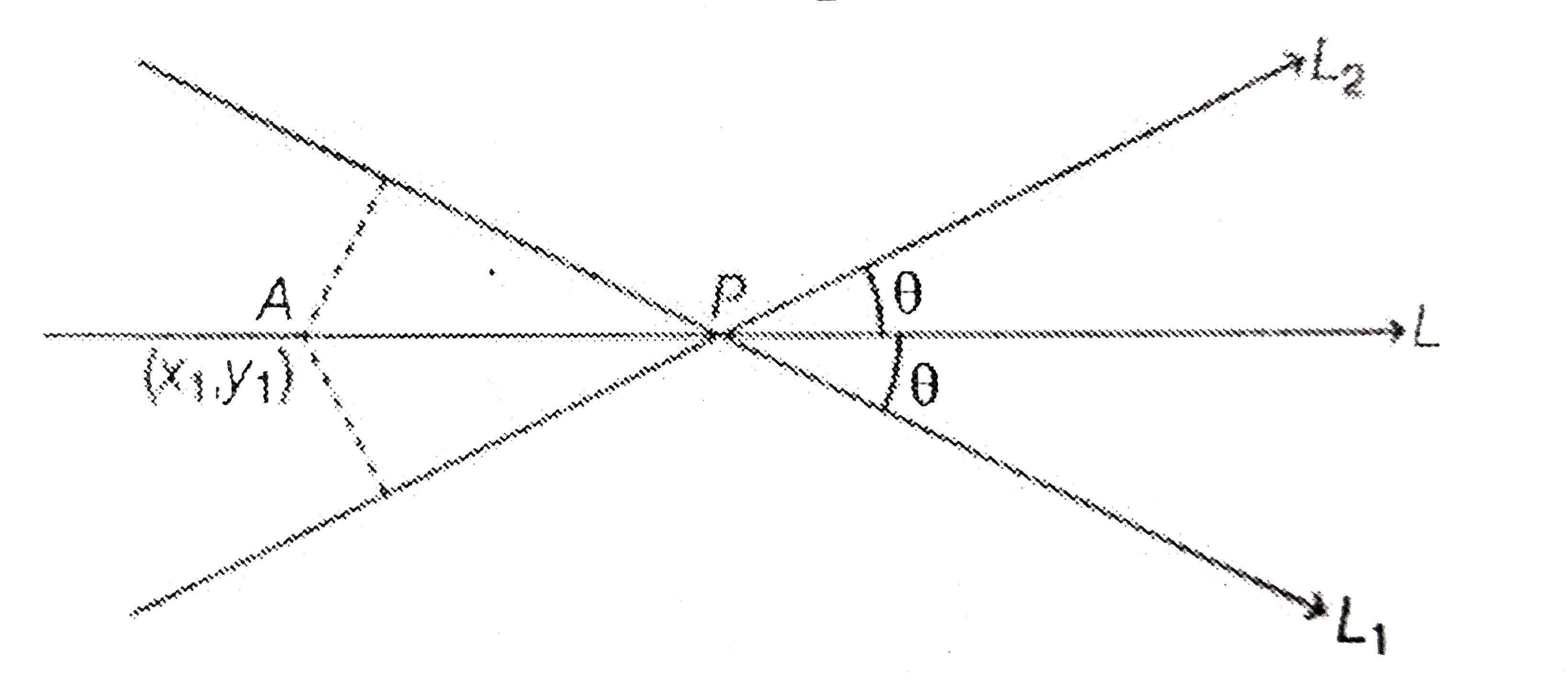
- Line L(1) -=ax+by+c=0 " and " L(2) -= lx+my+n=0 intersect at point P a...
Text Solution
|
- Lines L1-=a x+b y+c=0 and L2-=l x+m y+n=0 intersect at the point P and...
Text Solution
|
- In the xy plane,the line L(1) passes through the point (1,1) and the l...
Text Solution
|
- lines L(1):ax+by+c=0 and L(2):lx+my+n=0 intersect at the point P and m...
Text Solution
|
- theta(1) and theta(2) are the inclination of lines L(1) and L(2) with ...
Text Solution
|
- The line l(1) passing through the point (1,1) and the l(2), passes thr...
Text Solution
|
- Lines,L(1):x+sqrt(13y)=2, and L(2):ax+by=1 meet at P and enclose an an...
Text Solution
|
- If lines l(1), l(2) and l(3) pass through a point P, then they are cal...
Text Solution
|
- The combined equation of the lines L(1) and L(2) is 2x^(2)+6xy+y^(2)=0...
Text Solution
|