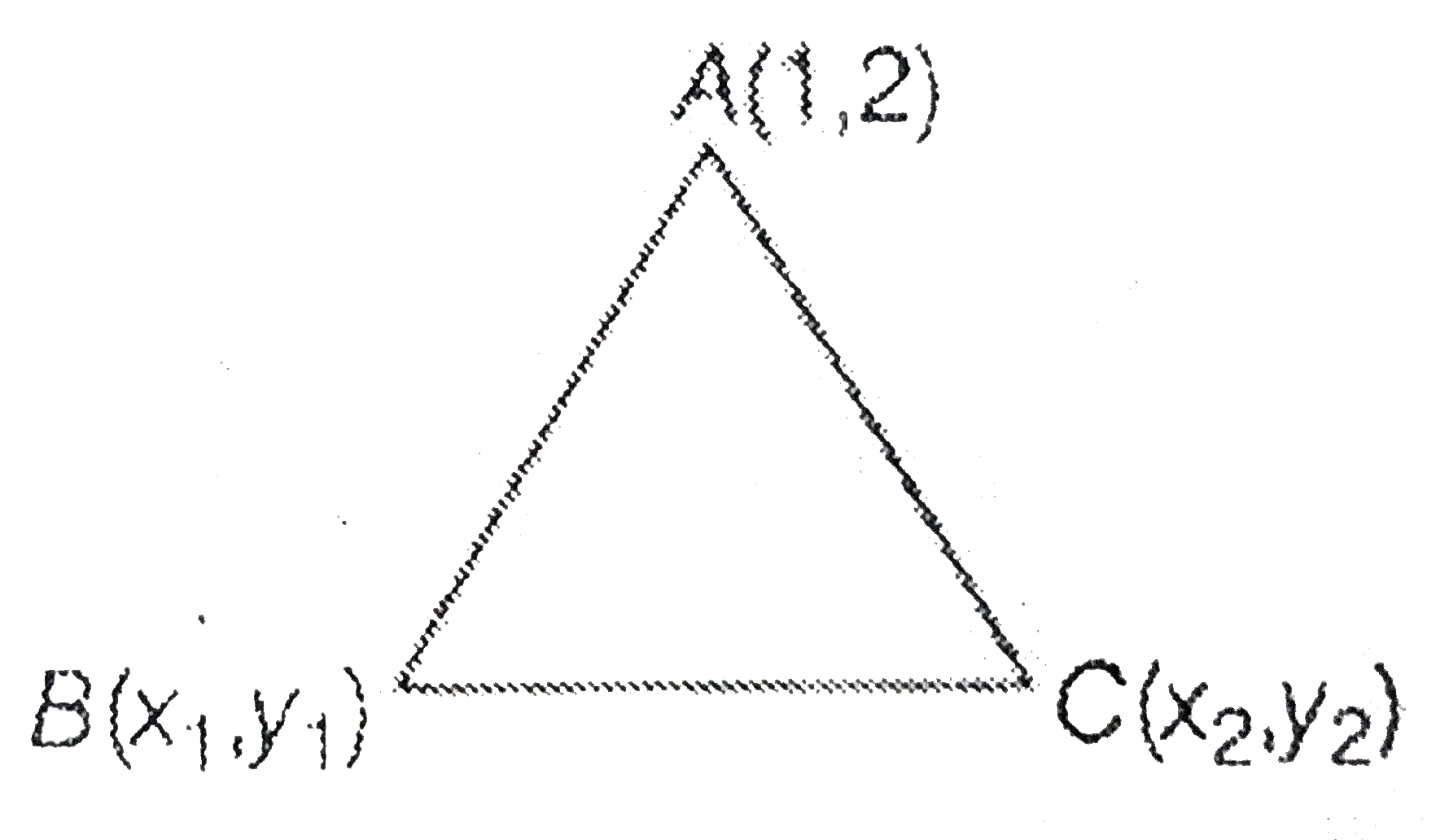
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- If a vertex of a triangle is (1, 1) and the mid points of two sides t...
Text Solution
|
- The points (1,-1),(2,-1) and (4,-3) are the mid-points of the sides of...
Text Solution
|
- It the mid-points of the sides of triangle are (1, 2, -3), (3, 0, 1)...
Text Solution
|
- If ((3)/(2),0), ((3)/(2), 6) and (-1, 6) are mid-points of the sides o...
Text Solution
|
- If a vertex of a triangle is (1, 1) and the mid-points of two side thr...
Text Solution
|
- If the vertex of a triangle is (1,1) and the mid-points of two sides t...
Text Solution
|
- The coordinates of the vertex A of the triangle ABC are (2,5), if the ...
Text Solution
|
- If a vertex of a triangle is (1, 1) and the midpoints of two sides thr...
Text Solution
|
- If a vertex of a triangle is (1, 1) and the mid-points of two sides th...
Text Solution
|