A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
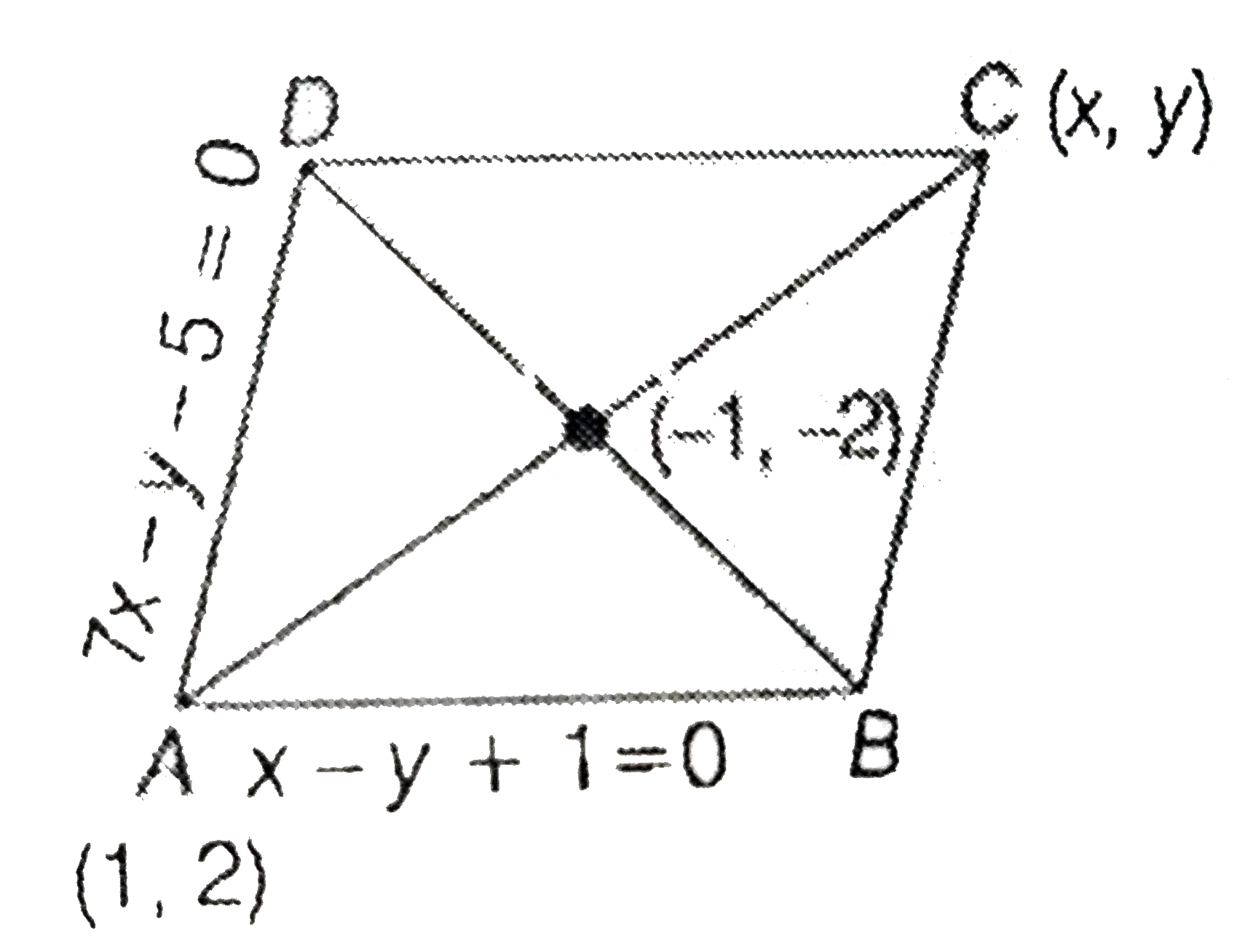
- Two sides of a rhombus are along the lines x-y+1=0 and 7x-y-5=0. If it...
Text Solution
|
- Two sides of a rhombus are along the lines, x-y+1=0 and 7x-y-5=0. If i...
Text Solution
|
- Two sides of a rhombus are along the lines,x-y+1=0 and 7x-y-5=0 . If...
Text Solution
|
- Two sides of a rhombus are along the lines x - y + 1 = 0 and 7 x - y ...
Text Solution
|
- The sides of a rhombus ABCD are parallel to the lines x−y+2=0 and 7x−y...
Text Solution
|
- यदि एक समचतुर्भुज की दो भुजाएं रेखाओ x-y +1 =0 तथा 7x - y- 5=0 की दिश...
Text Solution
|
- একটি রম্বসের দুটি বাহু x-y + 1 = 0এবং7x-y- 5 = 0 সরলরেখাদ্বয়ের অংশবি...
Text Solution
|
- Two sides of a rhombus ABCD are parallel to the lines y = x + 2 and y ...
Text Solution
|
- Two sides of a rhombus ABCD are parallel to the lines y = x + 2 and y ...
Text Solution
|