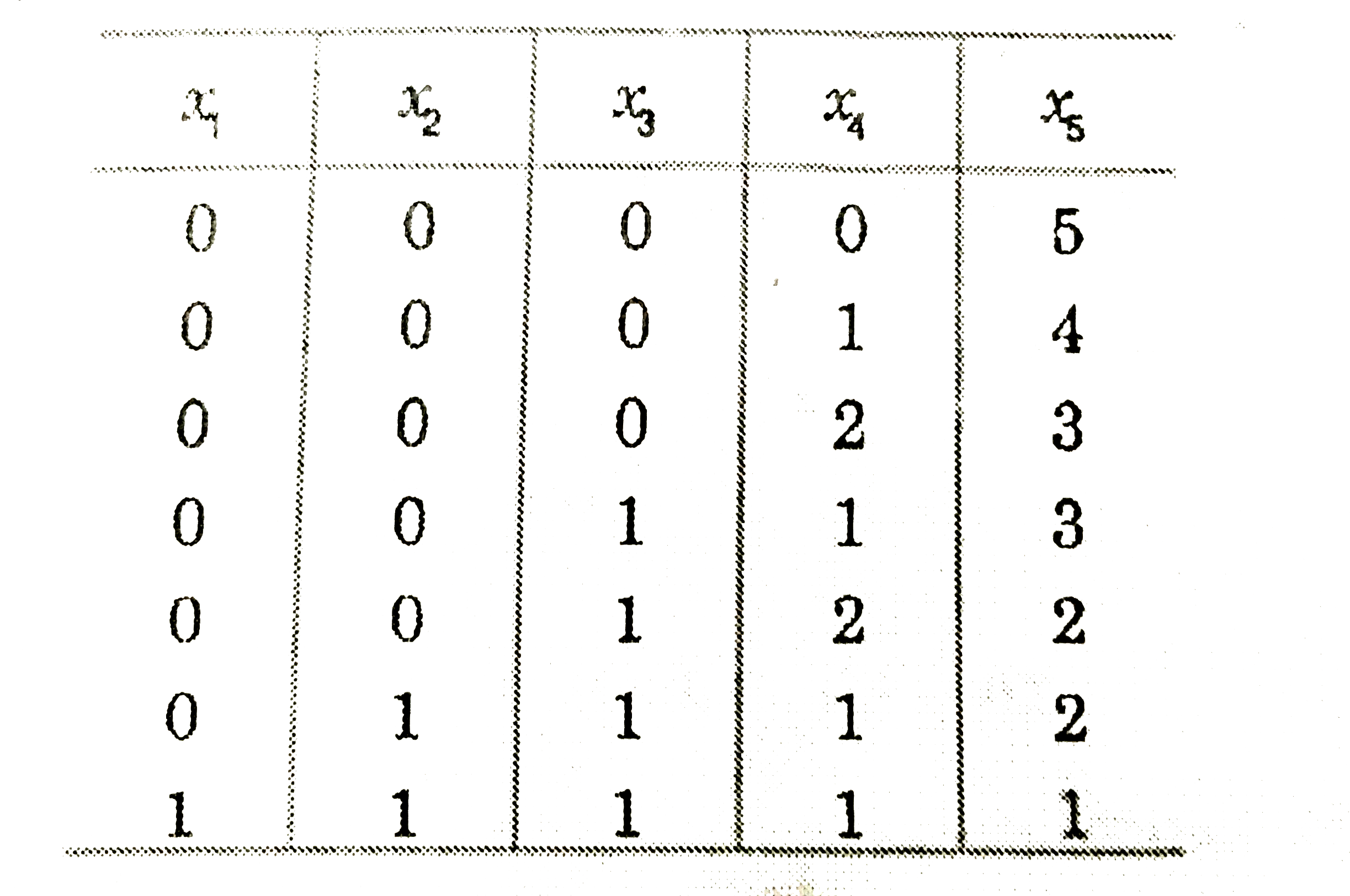
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let n1<n2<n3<n4<n5 be positive integers such that n1+n2+n3+n4+n5=20...
Text Solution
|
- Four numbers n1,n2,n3a n dn4 are given as n1=sin15^0-cos15^0,n2=cos93^...
Text Solution
|
- Let n1ltn2ltn3ltn4ltn5 be positive integers such that n1+n2+n3+n4+n5=2...
Text Solution
|
- Four numbers n1,n2,n3andn4 are given as n1=sin15^@-cos15^@,n2=cos93^@+...
Text Solution
|
- Assertion : The transition of electrons n3 to n2 in H atom will emit g...
Text Solution
|
- If S1 ,S2 and S3 denote the sum of first n1,n2 and n3 terms respec...
Text Solution
|
- यदि n1 lt n2 lt n3 lt n4 lt n5 इस प्रकार के धनात्मक पूर्णाक है जिनके ...
Text Solution
|
- Four numbers n1,n2,n3a n dn4 are given as n1=sin15^0-cos15^0,n2=cos93^...
Text Solution
|
- Let n1ltn2ltn3ltn4ltn5 be positive integers such that n1+n2+n3+n4+n5="...
Text Solution
|