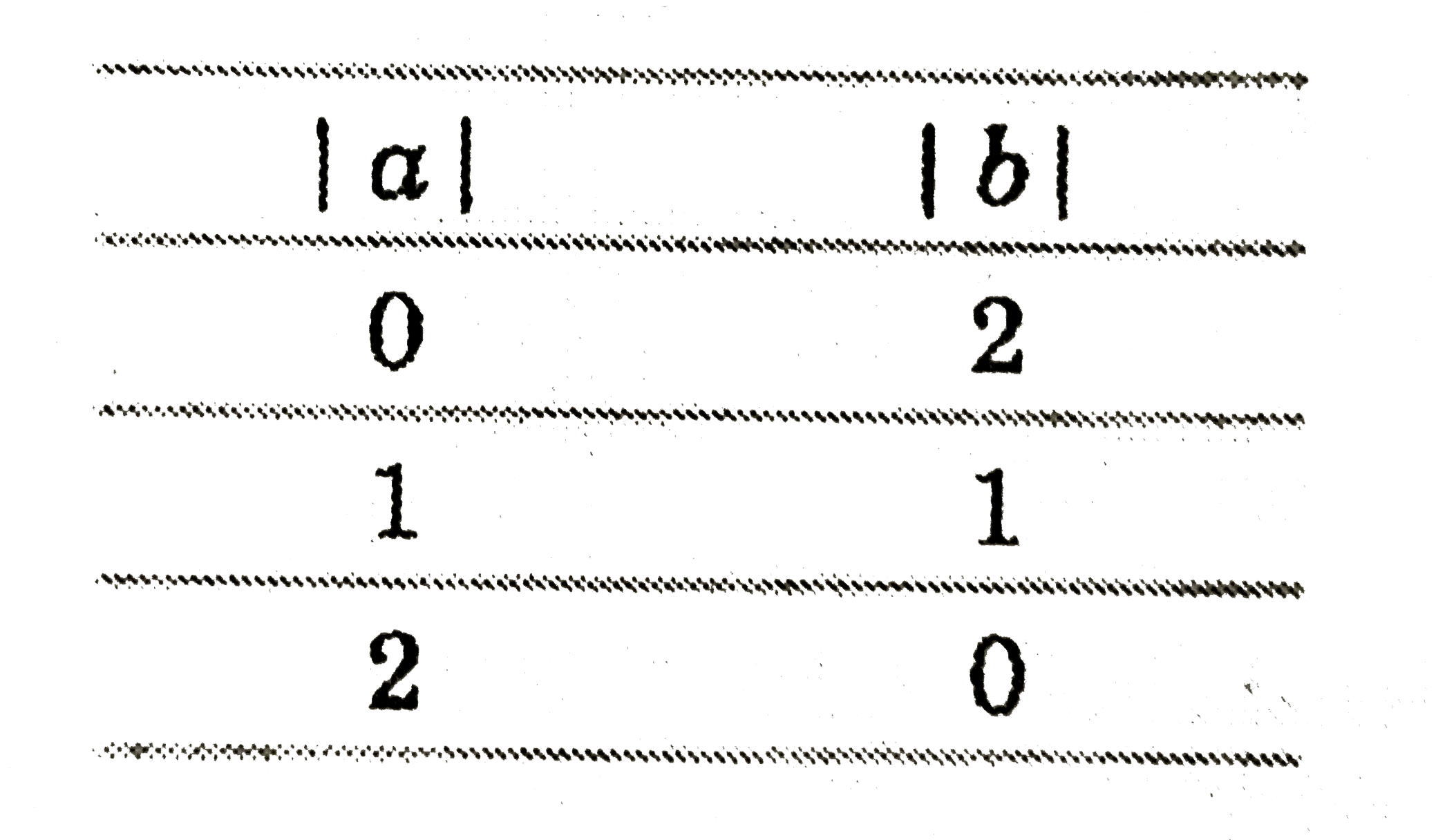A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If S is a set of triangles whose one vertex is origin and other two ve...
Text Solution
|
- Two vertices of a triangle are A(2,1) and B(3,-2). The third vertex C ...
Text Solution
|
- If S is a set of triangles whose one vertex is origin and other two ve...
Text Solution
|
- The area of a triangle is 3 square units. Two of its vertices are A (3...
Text Solution
|
- Let S be the set of all triangles in the xy-plane, each having one ver...
Text Solution
|
- एक त्रिभुज का क्षेत्रफल 3 वर्ग इकाई है इसके दो शीर्षों के निर्देशांक A...
Text Solution
|
- किसी त्रिभुज के दो शीर्षों के निर्देशांक (-8, 7) और (9, 4) हैं । य...
Text Solution
|
- Let "S" be the set of all triangles in the xy-plane,each having one v...
Text Solution
|
- माना S xy-तल में स्थित ऐसी सभी त्रिभुजों का समुच्चयों है जिनका एक शीर्...
Text Solution
|