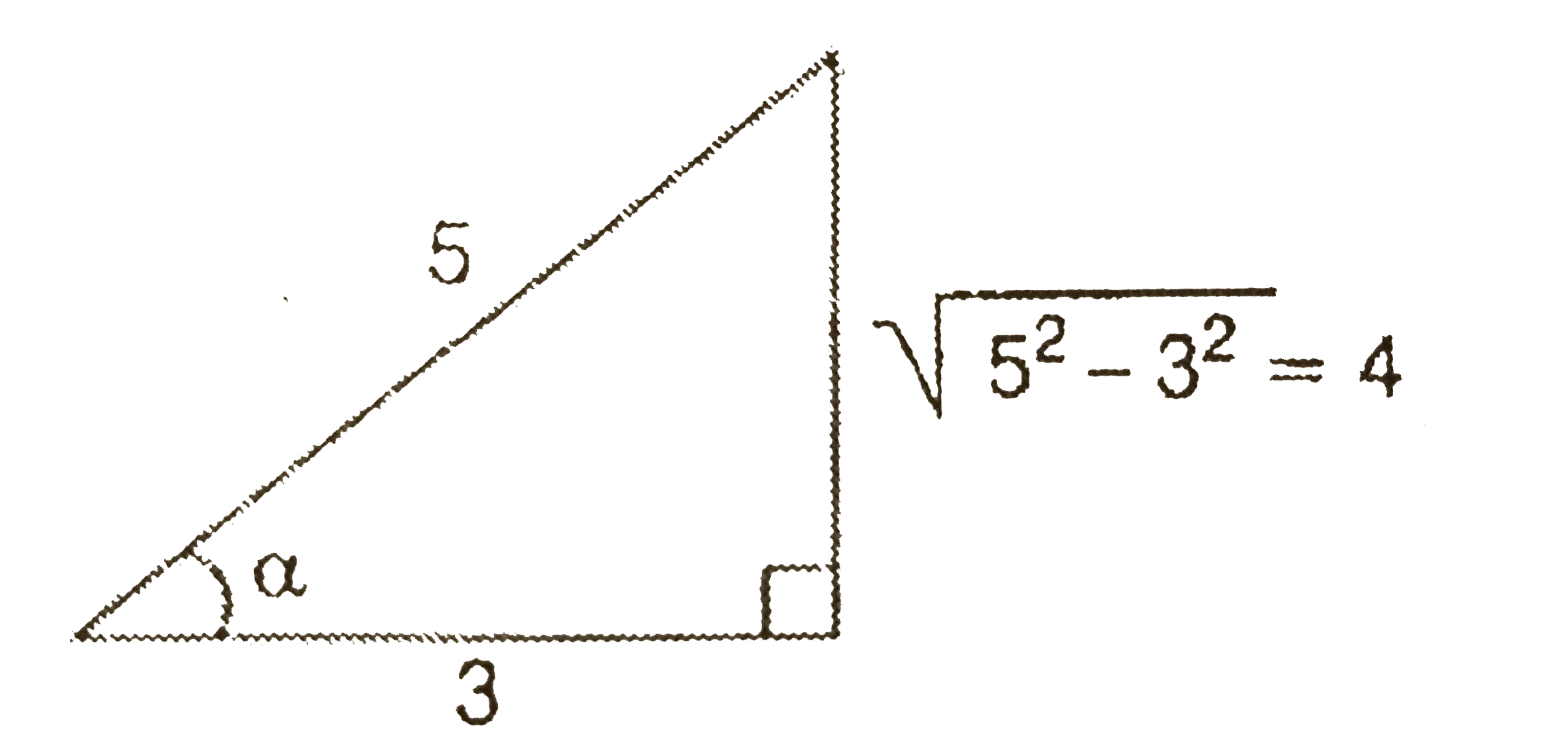A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
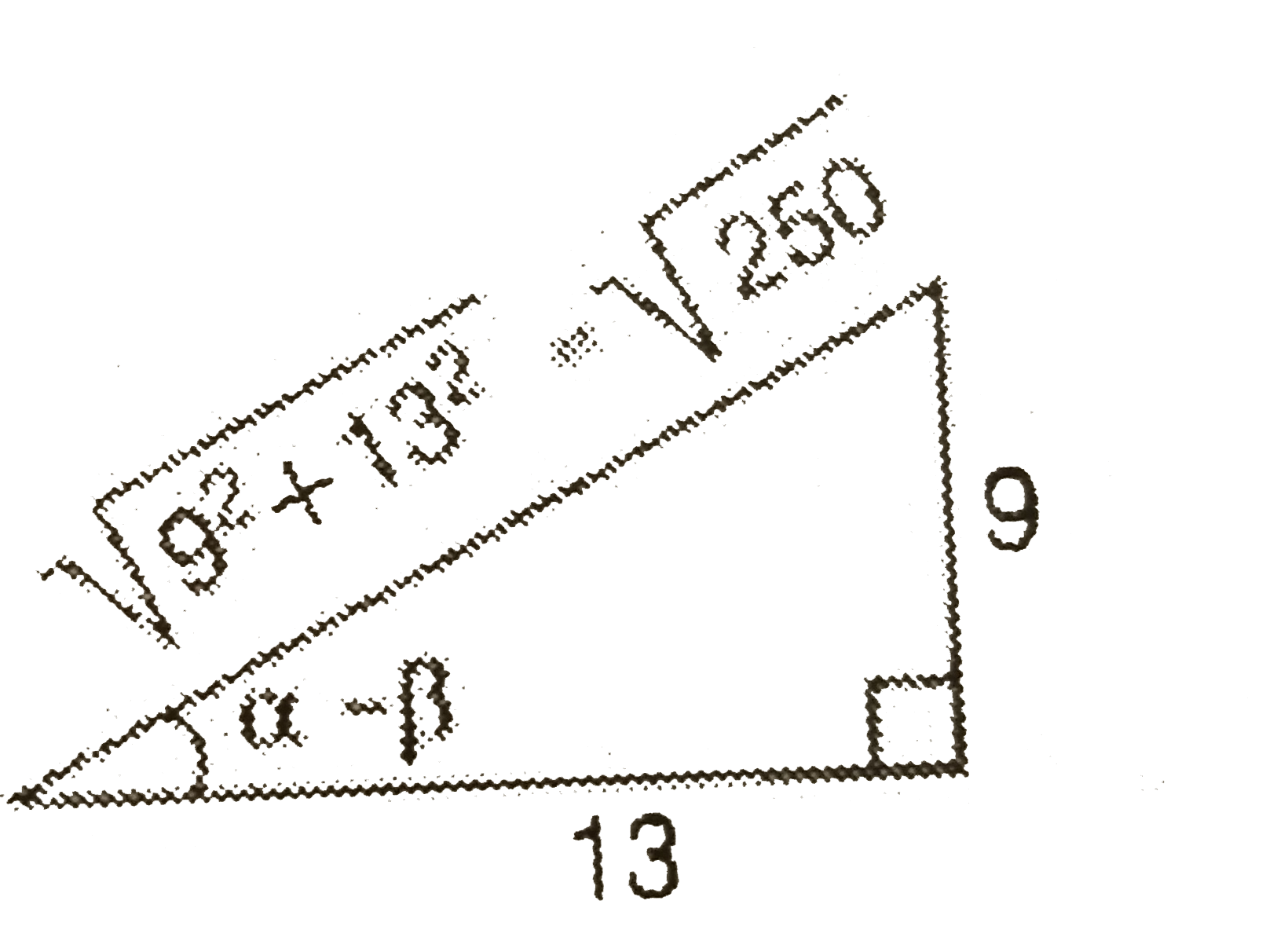
- If alpha = cos^(-1)((3)/(5)), beta = tan ^(-1)((1)/(3)) , where 0 lt a...
Text Solution
|
- If alpha=cos^(-1)((3)/(5)),beta=tan^(-1)((1)/(3)), where 0ltalpha,beta...
Text Solution
|
- If cos(alpha+beta)=3/5, sin(alpha-beta)=5/13, and 0 lt alpha, beta lt ...
Text Solution
|
- If alpha = cos^(-1)((3)/(5)), beta = tan ^(-1)((1)/(3)) , where 0 lt a...
Text Solution
|
- यदि alpha = cos^(-1)(4/5), beta = tan^(-1)(2/3),0 lt alpha, beta lt pi...
Text Solution
|
- यदि alpha = cos^(-1)(4/5), beta = tan^(-1)(2/3),0 lt alpha, beta lt pi...
Text Solution
|
- यदि cos(alpha + beta) = 3/5, sin(alpha - beta) = 5/13 तथा 0 lt alpha, ...
Text Solution
|
- यदि alpha = cos^(-1) ((3)/(5)), beta = tan^(-1) ((1)/(3)) जहाँ 0 lt a...
Text Solution
|
- If cos(alpha + beta) = 3/5, sin(alpha - beta) = 5/13 And 0 lt alpha, b...
Text Solution
|