A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
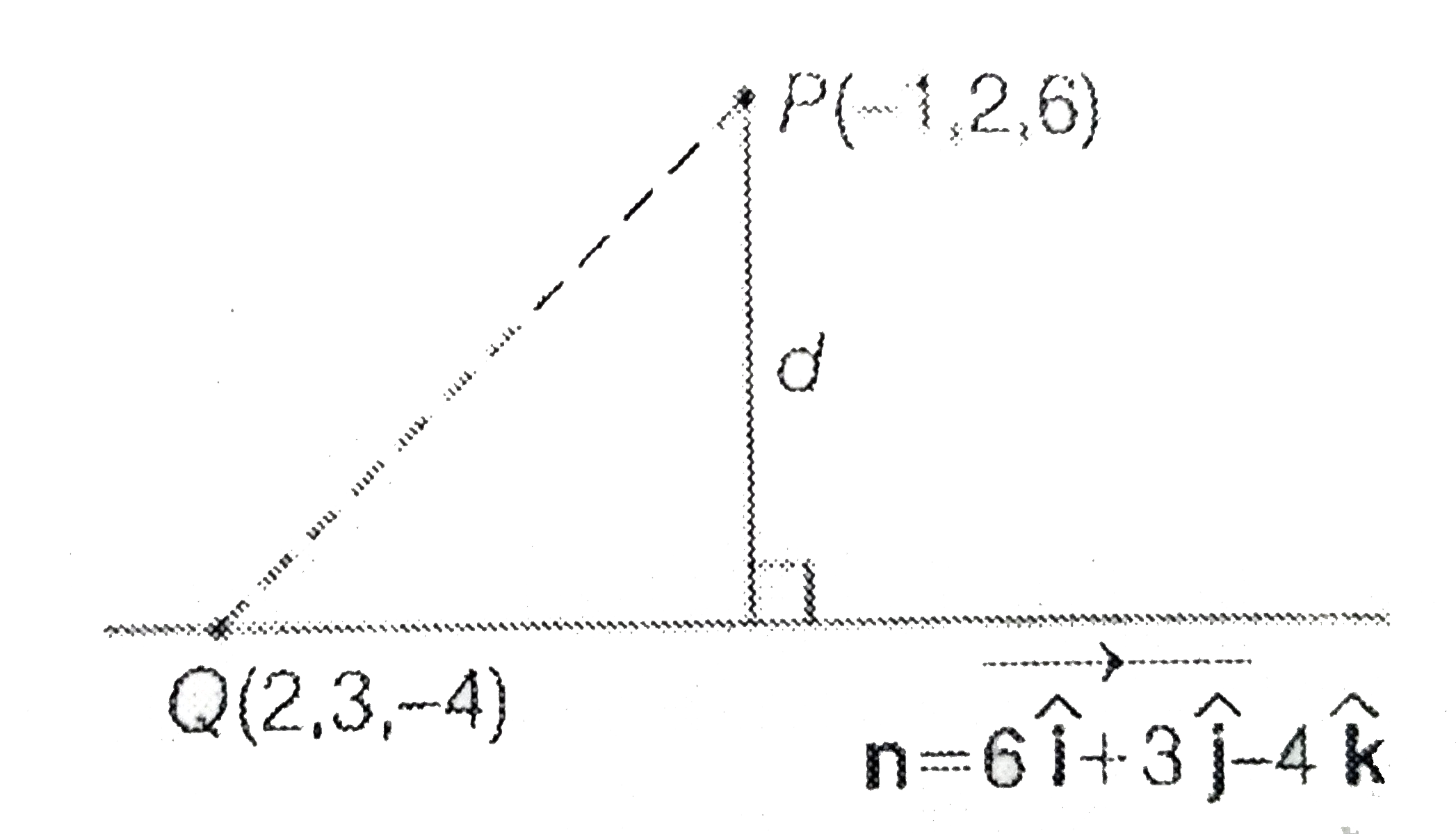
- The distance of the point (-hati+2hatj+6hatk) from the straight line t...
Text Solution
|
- The distance of the point -i+2j+6k from the straight line through the ...
Text Solution
|
- Find the perpendicular distance of P(-hati+2hatj+6hatk) from the line ...
Text Solution
|
- The distance from the point -hati+2hatj+6hatk to the straight line thr...
Text Solution
|
- Find the vector and Cartesian equations of the plane passing through t...
Text Solution
|
- The distance of the point 3hati+5hatk from the line parallel to 6hati+...
Text Solution
|
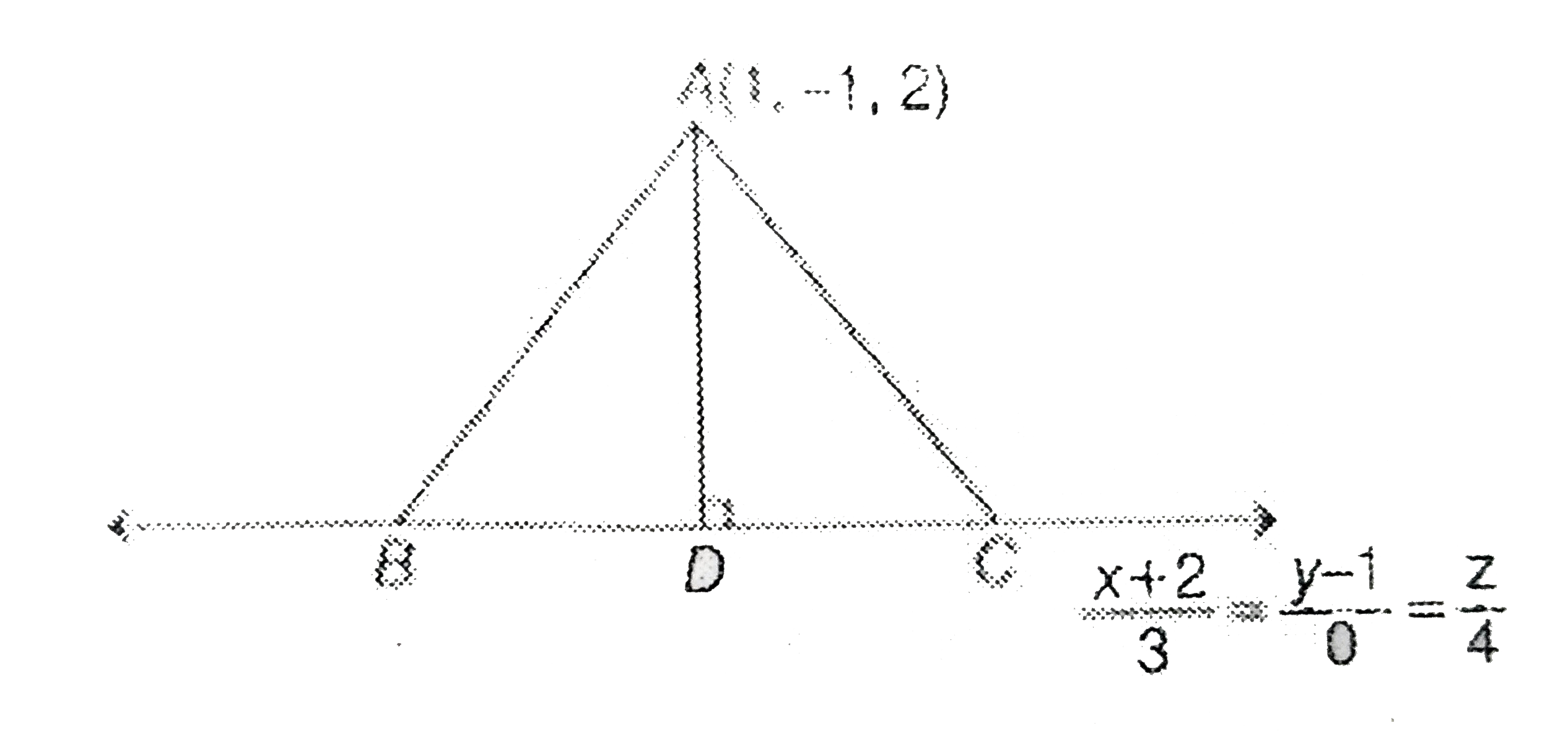
- The distance of the point P(1,2,3) from the line which passes through ...
Text Solution
|
- दर्शाइए की रेखाएं vecr = hati+2hatj-3hatk+lamda(2hati+hatj+2hatk) और...
Text Solution
|
- उस सरल रेखा का सदिश समीकरण ज्ञात कीजिए जो सदिश 3hati +2hatj +6hatk के...
Text Solution
|