A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
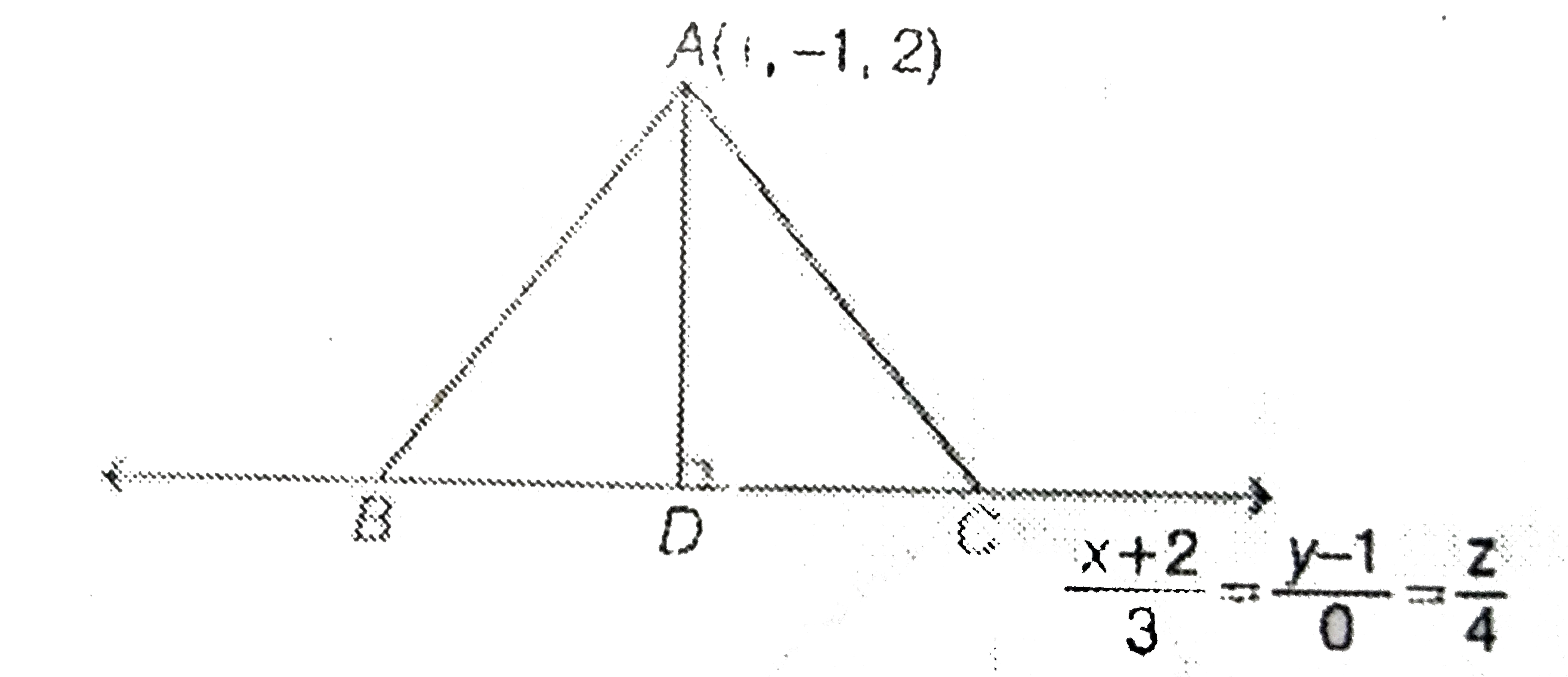
- The vertices B and C of a DeltaABC lie on the line, (x+2)/(3)=(y-1)/(0...
Text Solution
|
- Thangents are drawn from (-1, 0) to y^2 = 4x. Then the area of the tri...
Text Solution
|
- The area bounded by the parabola y=(x+1)^2 and y=(x-1)^2 and the line ...
Text Solution
|
- If two points B and C at distance of 5 units from each other, lie on t...
Text Solution
|
- The vertices B and C of a DeltaABC lie on the line, (x+2)/(3)=(y-1)/(0...
Text Solution
|
- A ( 1, - 1) , B(2frac{1}{2},0) , C (4 , 1) then area of DeltaABC ...
Text Solution
|
- The area (in sq. units ) of the triangle formed by the lines x^(2) - 3...
Text Solution
|
- Delta ABC के शीर्ष B तथा C रेखा (x+2)/(3)=(y-1)/(0)=(2)/(4) पर स्थित...
Text Solution
|
- If the vertices of a Delta ABC are A = (2, 3, 5), B = (-1, 3, 2), C = ...
Text Solution
|