A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
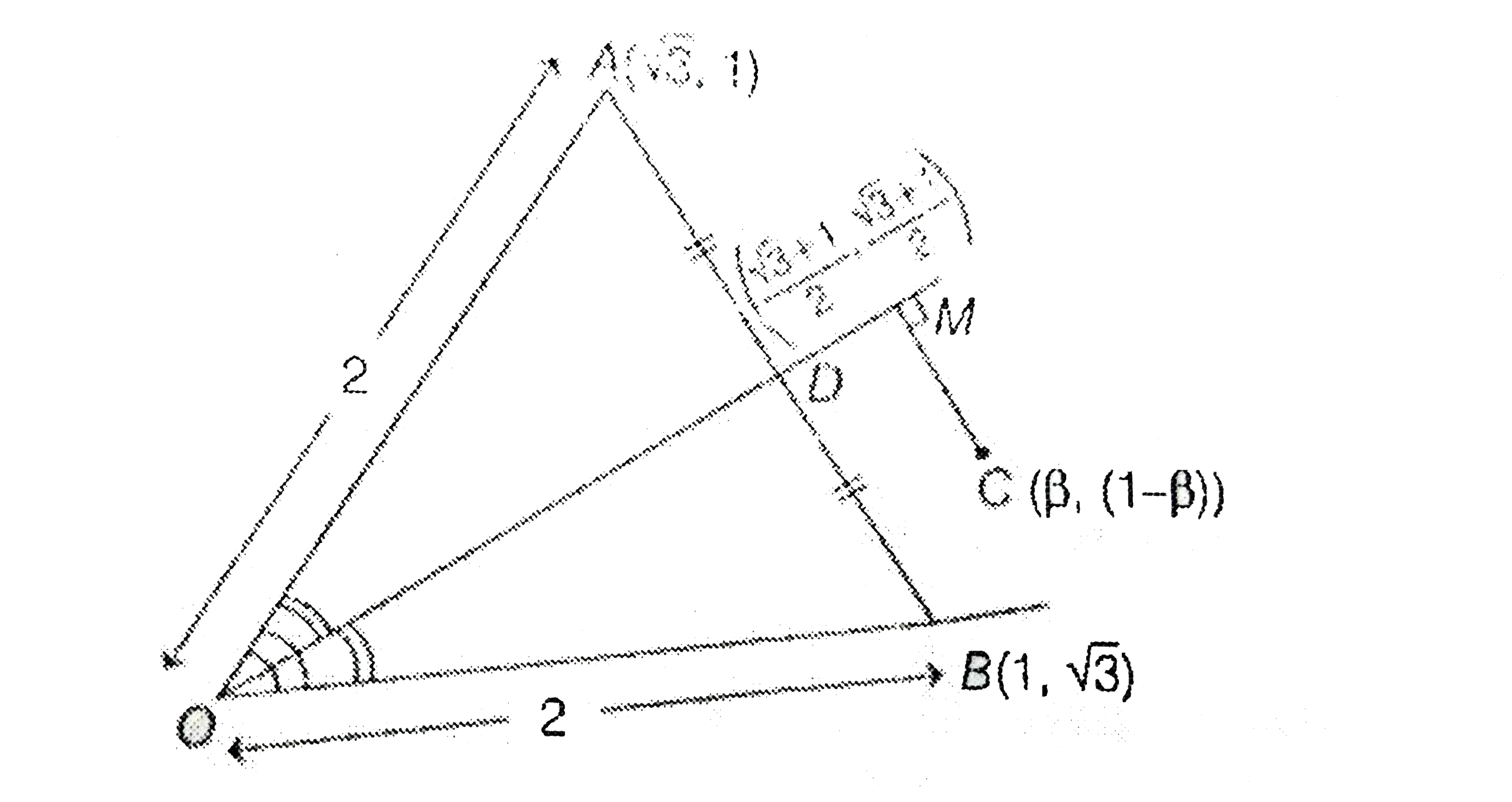
- Let sqrt(3)hati+hatj,hati+sqrt(3)hatj" and "betahati+(1-beta)hatj resp...
Text Solution
|
- Let veca=hati-hatj, vecb=hatj-hatk, vecc=hatk-hati. If hatd is a unit ...
Text Solution
|
- Let sqrt(3)hati+hatj,hati+sqrt(3)hatj" and "betahati+(1-beta)hatj resp...
Text Solution
|
- The position vectors of the points A, B, C are 2 hati + hatj - hatk , ...
Text Solution
|
- Let a=hati+hatj+hatk, b=hati-hatj+hatkandc=hati-hatj-hatk be three vec...
Text Solution
|
- Let sqrt(3i) + hatj , hati + sqrt(3j) and beta hati + (1- beta)hatj r...
Text Solution
|
- If vector vec a = hati + hatj + hatk , vecb = 4 hati + 3 ...
Text Solution
|
- यदि a=hati+hatj+hatk, b=4hati+3hatj+4hatk तथा c=hati+alpha hatj+beta h...
Text Solution
|
- In R^2 let sqrt(3i) + hatj , hati + sqrt(3j) and beta hati + (1- beta...
Text Solution
|