A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
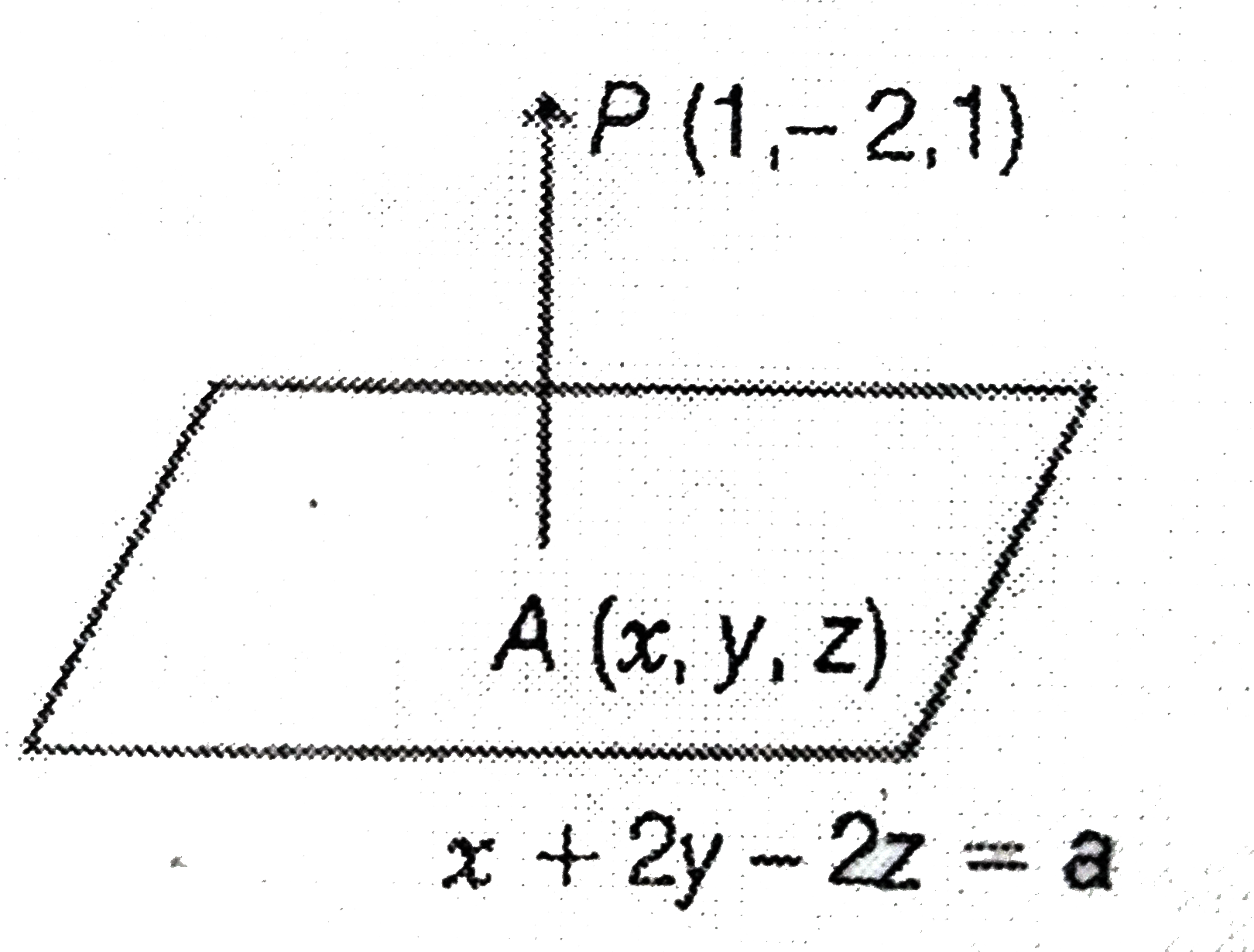
- If the distance of the point P(1,-2,1) from the plane x+2y-2z=alpha...
Text Solution
|
- If the distance of the point P(1,-2,1) from the plane x+2y-2z=alpha...
Text Solution
|
- The coordinates of the foot of the perpendicular from the point (1,-2,...
Text Solution
|
- If P(2,3,1) is a point L-=x-y-z-2=0 is a plane then (A) origin and P l...
Text Solution
|
- Let A(1, 1, 1), B(3, 7, 4) and C (-1, 3, 0) be three points in a pla...
Text Solution
|
- बिंदु P(1, 2, 4) से समतल 2x + y -2z + 3 = 0 पर लम्ब डाला जाता है | ...
Text Solution
|
- The coordinates of the foot of the perpendicular from the point (1,-2...
Text Solution
|
- (3, 4, 3) এবং (2,1, 5) বিন্দু দুটির সংযোজক সরলরেখা 2x+ 2y- 2z = 1 সমতল...
Text Solution
|
- If the distance of the point P(1,-2,1) from the plane x+2y-2z=alpha,...
Text Solution
|