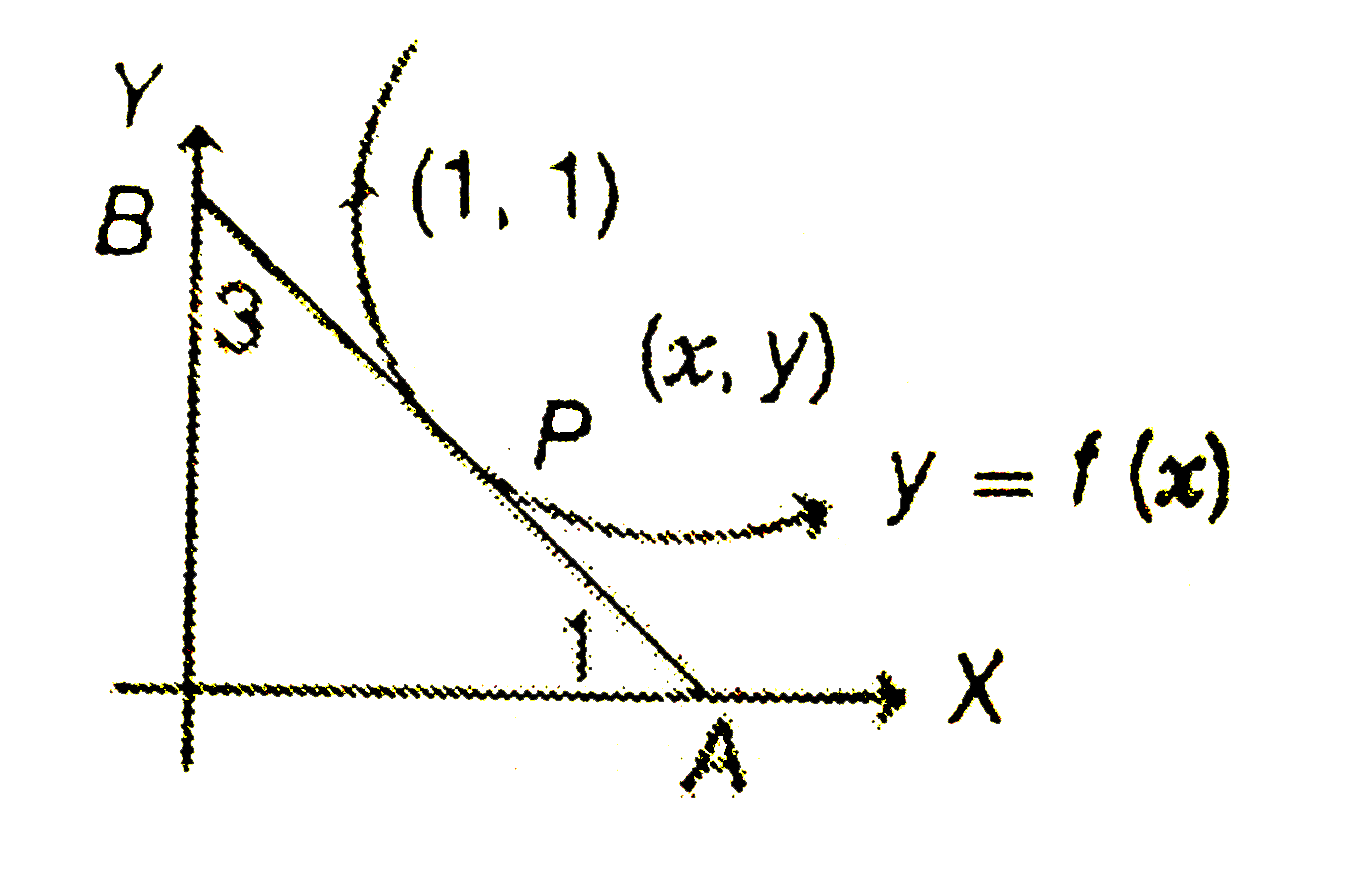A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Tangent is drawn at any point P of a curve which passes through (1, 1)...
Text Solution
|
- Find the equation of the tangent to the curve y=(x^3-1)(x-2) at the po...
Text Solution
|
- A normal is drawn at a point P(x , y) of a curve. It meets the x-axis...
Text Solution
|
- Tangent is drawn at any point P of a curve which passes through (1,1) ...
Text Solution
|
- A tangent drawn to the curve y=f(x) at P(x,y) cuts the x-axis and y-ax...
Text Solution
|
- A tangent drawn to the curve y = f(x) at P(x, y) cuts the x and y axes...
Text Solution
|
- एक वक्र बिन्दु (1,1) से होकर जाता है तथा इसके किसी बिन्दु P पर एक स्पर...
Text Solution
|
- एक वक्र के किसी बिन्दु P पर एक स्पर्शी खींची जाती है, जोकि (1,1) से ह...
Text Solution
|
- The slope of the tangent to the curve x^(3)-x+1 at the point where the...
Text Solution
|