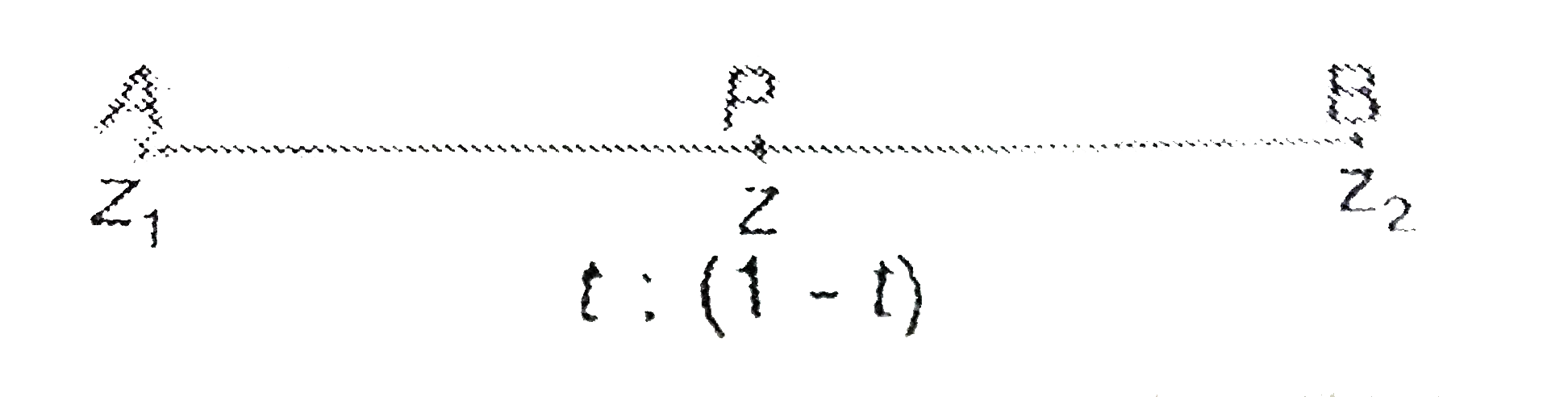Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let z1 and z2 be two distinct complex numbers and let z=(1-t)z1+t z2...
Text Solution
|
- Statement-1 If|z1| and |z2| are two complex numbers such that |z1|=|z2...
Text Solution
|
- If z, z1 and z2 are complex numbers, prove that (i) arg (barz) = - arg...
Text Solution
|
- If z1 and z2 are two non- zero comlex numbers such that |z1+z2|=|z1|...
Text Solution
|
- Complex number z1 and z2 satisfy z+barz=2|z-1| and arg (z1-z2) = pi/4 ...
Text Solution
|
- यदि |z1 + z2 | = | z1 - z2 | हो, तो "Arg"(z1)"-Arg"(z2) का मान होगा |
Text Solution
|
- If z1 & z2 are two complex number & if arg (z1+z2)/(z1-z2)=pi/2 but |z...
Text Solution
|
- If z1 And z2 Let the two nonzero complex numbers be |z1+z2|=|z1|+|z2| ...
Text Solution
|
- If z1,z2 ,….. zn=z , Then arg z1+arg z2 +….+ arg zn And arg z will be ...
Text Solution
|