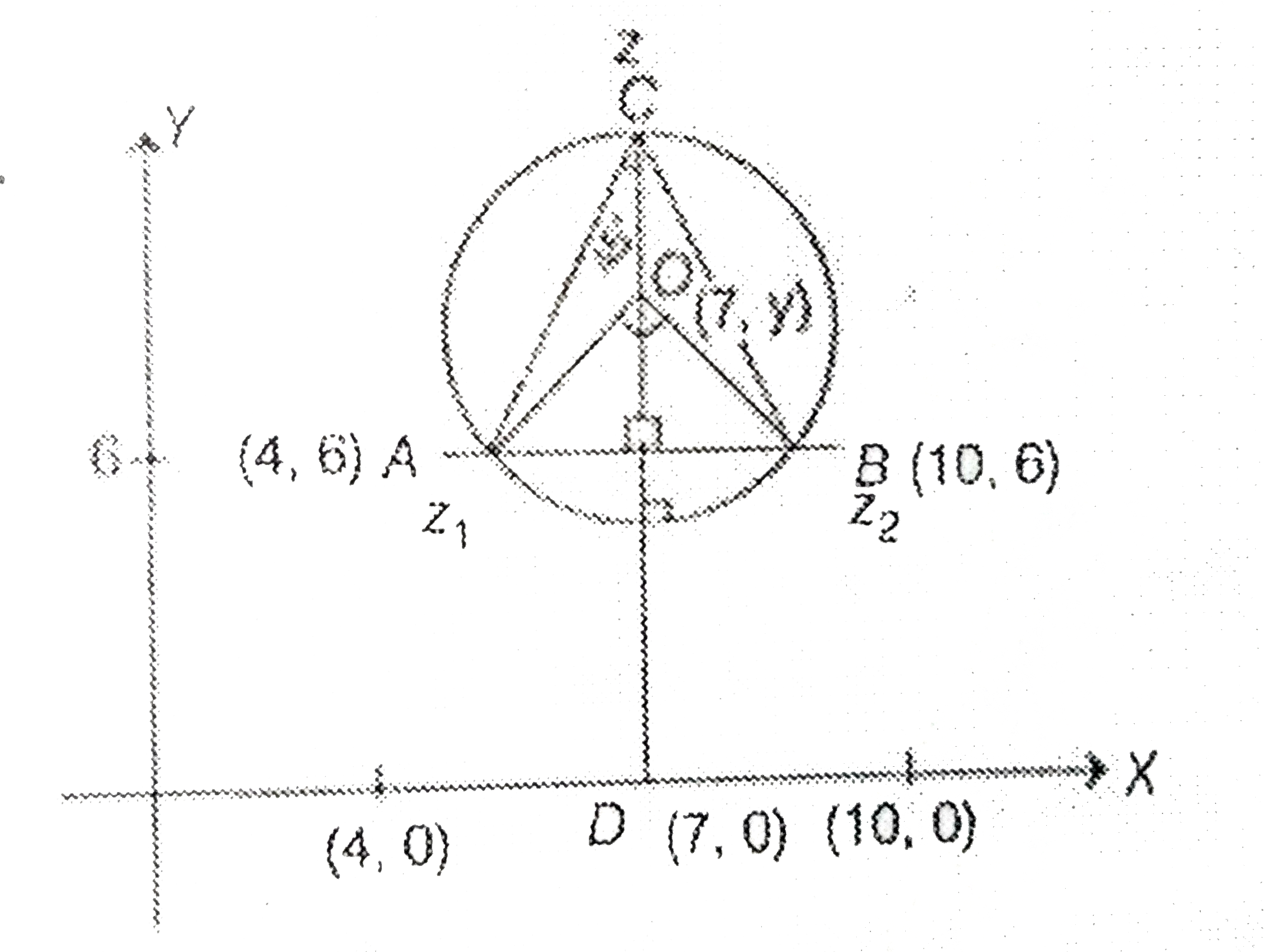Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let z1=10+6i and z2=4+6idot If z is any complex number such that the a...
Text Solution
|
- Let z(1)=10+6i and z(2)=4+6i. If z is a complex number such that the a...
Text Solution
|
- If z1=10+6iandz2=4+2i be two complex numbers and z be a complex number...
Text Solution
|
- Complex number z1 and z2 satisfy z+barz=2|z-1| and arg (z1-z2) = pi/4 ...
Text Solution
|
- यदि |(z-z1)//(z-z2)|=3 , जहाँ z1 और z2 स्थिर सम्मिश्र संख्यायें तथा z...
Text Solution
|
- The maximum area of the triangle formed by the complex coordinates z,...
Text Solution
|
- Let z1a n dz2 be two distinct complex numbers and let z=(1-t)z1+t z2 f...
Text Solution
|
- Let z1=10+6i and z2=4+6idot If z is any complex number such that the a...
Text Solution
|
- Let z1, z2 , z3 in C such that |z1 | = |z2| = |z3| = |z1+ z...
Text Solution
|