A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
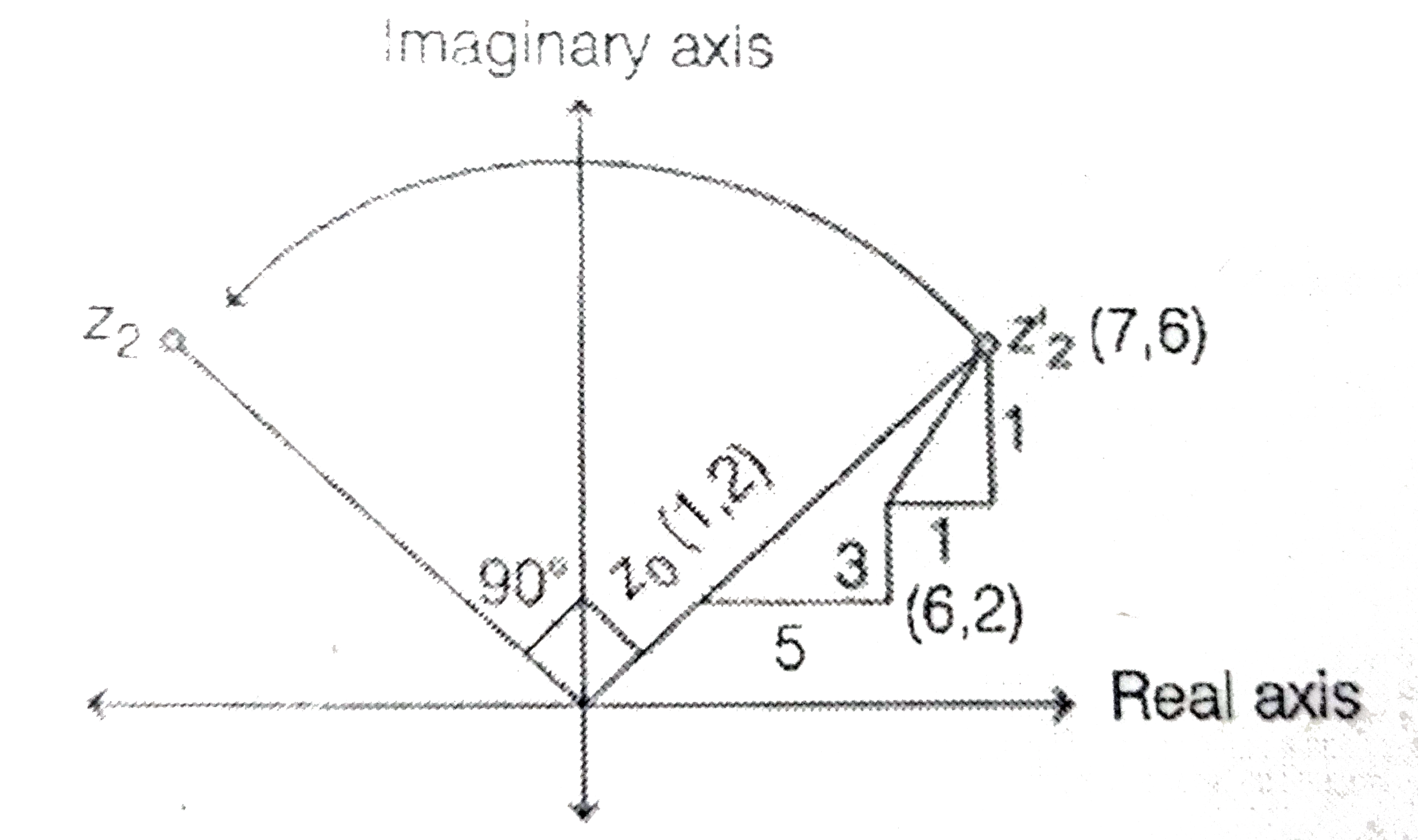
- A particle starts from a point z0=1+i where i=sqrt(-1). lt moves horiz...
Text Solution
|
- A particle P starts from the point z0=1+2i , where i=sqrt(-1) . It mov...
Text Solution
|
- A particle starts from a point z0=1+i where i=sqrt(-1). lt moves horiz...
Text Solution
|
- A constant force 3hat i+4hat j-5hat k acts on a particle at hat i+2hat...
Text Solution
|
- If the direction cosines of the line joining the origin and a point at...
Text Solution
|
- A particle P starts from the point z(0)=1+2i, where i=sqrt(-1). It mov...
Text Solution
|
- एक कण P, बिन्दु z0 = 1+ 2i से प्रारंभ होता है, जहाँ i=sqrt(-1) सर्वप्र...
Text Solution
|
- एक कण P, बिन्दु z0 = 1+ 2i से प्रारंभ होता है, जहाँ i=sqrt(-1) सर्वप्र...
Text Solution
|
- A particle P starts from the point z0=1+2i , where i=sqrt(-1) . It mov...
Text Solution
|