Home
Class 12
MATHS
A man walks a distance of 3 units from t...

A man walks a distance of 3 units from the origin towards north-east to reach position A. from there he walks a distance of 4 units towards North west to reach position P. Then position of P in argand plane is

A

`3e^(I pi 4)+4i`

B

`(3-4 i)e^(I pi 4)`

C

`(4 + 3 i)e^(I pi 4)`

D

`(3+4i )e^(I pi 4)`

Text Solution

Verified by Experts

The correct Answer is:
D
Let OA=3 so that the complex number associated with A si `3e^( ipi//4)`, If z is the complex number associated with P, then
`(z-3e^(ipi//34))/(0-3e^(ipi//4))=4/3e^(-pi//2)=-(4 i)/(3)`
`rArr 3 z-9e^(ipi//4)=12 ie^(ipi//4)`
`rArr z= (3+ 4 i)e^(ipi//4)`
Promotional Banner

Similar Questions

Explore conceptually related problems

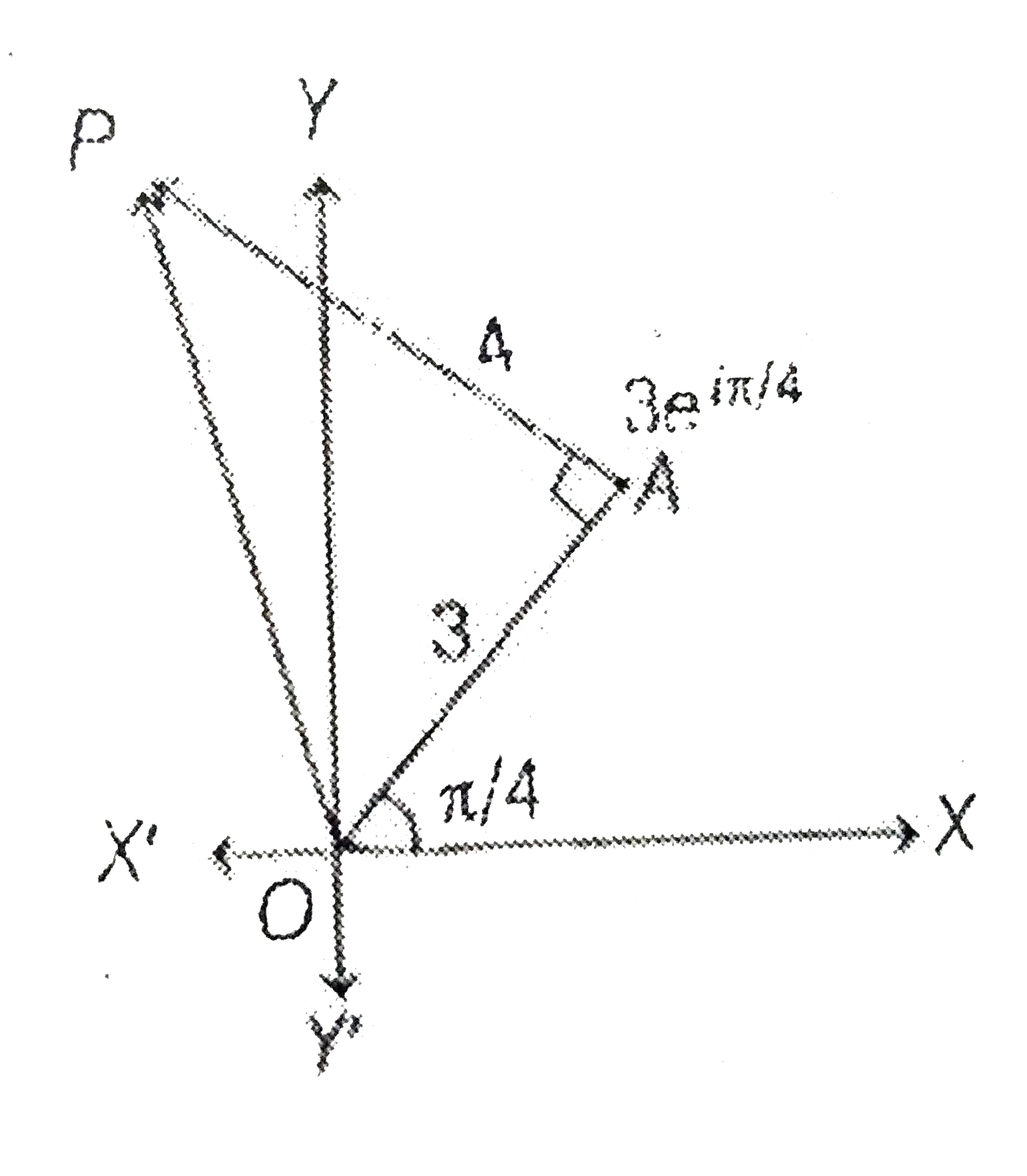
A man walks a distance of 3 units from the origin towards the North-East (N45^0E) direction.From there, he walks a distance of 4 units towards the North-West (N45^0W) direction to reach a point Pdot Then, the position of P in the Argand plane is 3e^((ipi)/4)+4i (b) (3-4i)e^((ipi)/4) (4+3i)e^((ipi)/4) (d) (3+4i)e^((ipi)/4)

A plane is at a distance 3 units from the origin. The direction ratios of normal to the plane are 1,-2,1. Find the vector and cartesian equation of the plane.

A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point ?

A man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?

The equation of the plane at a distance P from the origin and perpendicular to the unit normal vector hat(d) is

Find the vector equation of a plane with is at a distance of 7 units from the origin and normal to the vector 3hati+5hatj-6hatj .

on a cartesign plane, draw a line segment XY parallel to x -axis at a distance of 5 units from x -axis and a line segment PQ parallel to y -axis at a distance of 3 units from y -axis .write the co-ordinates of their point of intersection.

A man goes 3 km towards north and then 4 km towards east. How far is he away from the initial poisition ?

Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30^(@) with positive direction of the x-axis.