Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
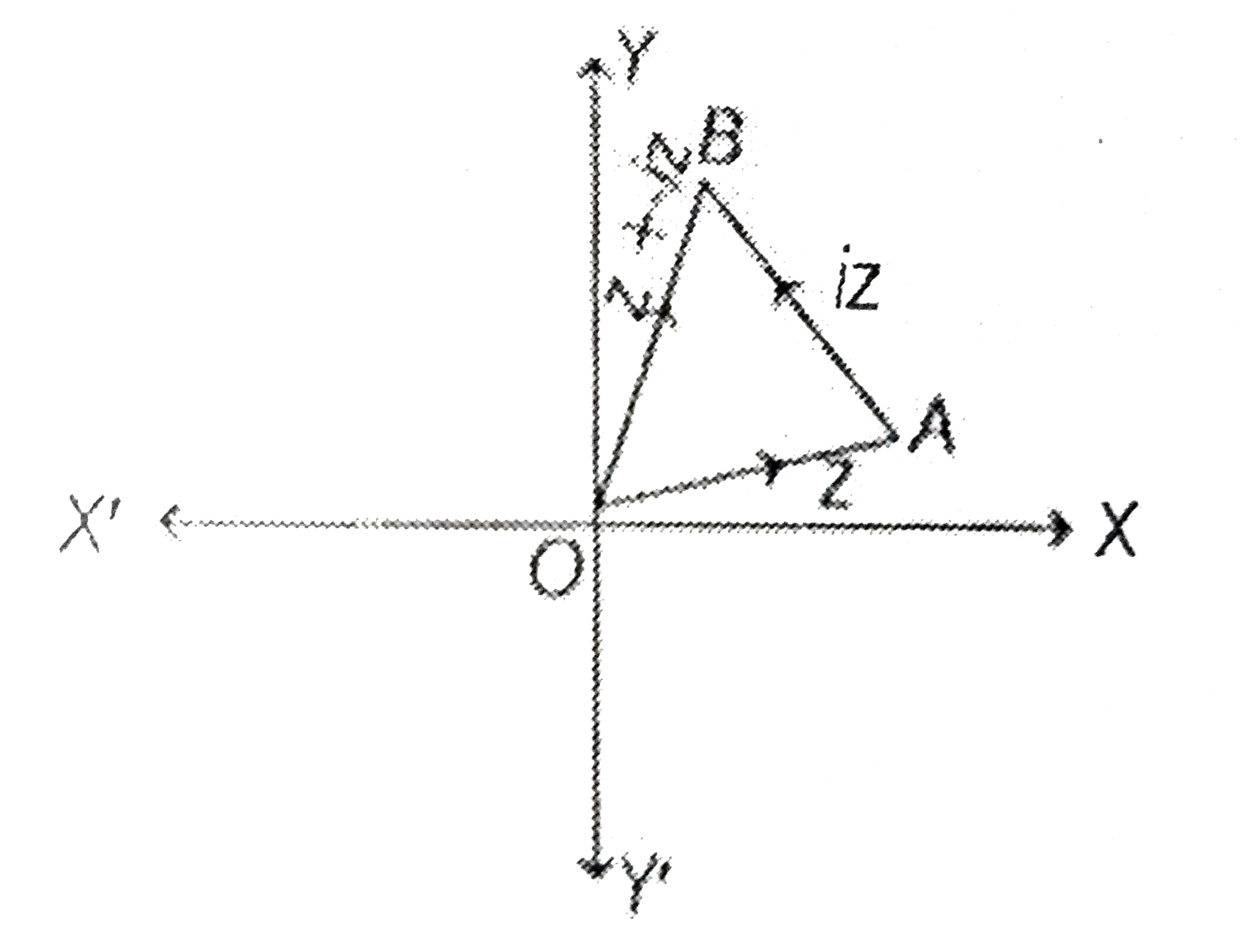
- Show that the area of the triangle on the Argand diagram formed by the...
Text Solution
|
- Show that the area of the triangle on the Argand diagram formed by the...
Text Solution
|
- Show that the area of the triagle on the argand plane formed by the co...
Text Solution
|
- Show that the area of the triangle on the Argrand Diagram formed by th...
Text Solution
|
- A : Area of triangle formed by 1+i,-1+I,2i" is " '1' square unit R :...
Text Solution
|
- दिखाइए कि सम्मिश्र संख्याओं z, iz और z+iz द्वारा बने त्रिभुज के आर्...
Text Solution
|
- Area of the triangle in the Argand diagram formed by the complex numbe...
Text Solution
|
- Show that the area of the triangle on the Argand diagram formed by the...
Text Solution
|
- Show that the area of the triangle on the Argand diagram formed by the...
Text Solution
|