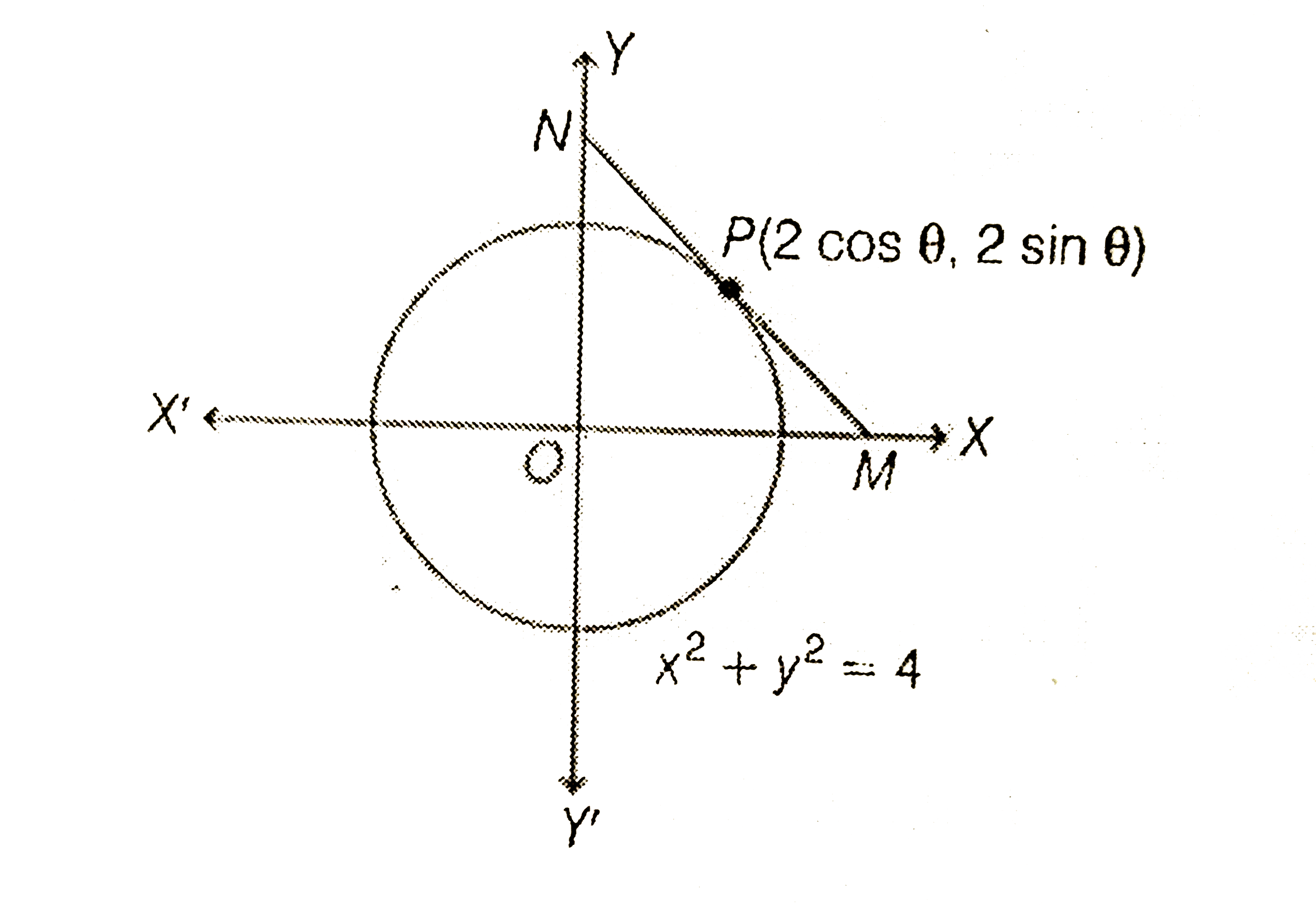A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let S be the circle in the x y -plane defined by the equation x^2+y^2=...
Text Solution
|
- Let O be the vertex and Q be any point on the parabola,x^2=""8y . I...
Text Solution
|
- A tangent at a point on the circle x^2+y^2=a^2 intersects a concentric...
Text Solution
|
- Let S={(x,y):(x^(2))/(9)+(y^(2))/(4)<=1} and T={(x,y):|x|<=3 and |y|<=...
Text Solution
|
- Let S={(x,y):(x^(2))/(9)+(y^(2))/(4)<=1} and T={(x,y):|x|<=3;|y|<=2}
Text Solution
|
- Let S be the circle in the x y -plane defined by the equation x^2+y^2=...
Text Solution
|
- Let P be any point on the curve x^(2//3)+y^(2//3)=a^(2//3). Then the...
Text Solution
|
- Let P be a point on the circle S with both coordinates being positive....
Text Solution
|
- P (-2,-1) and (0,-3) are the limiting points of a coaxial system of wh...
Text Solution
|