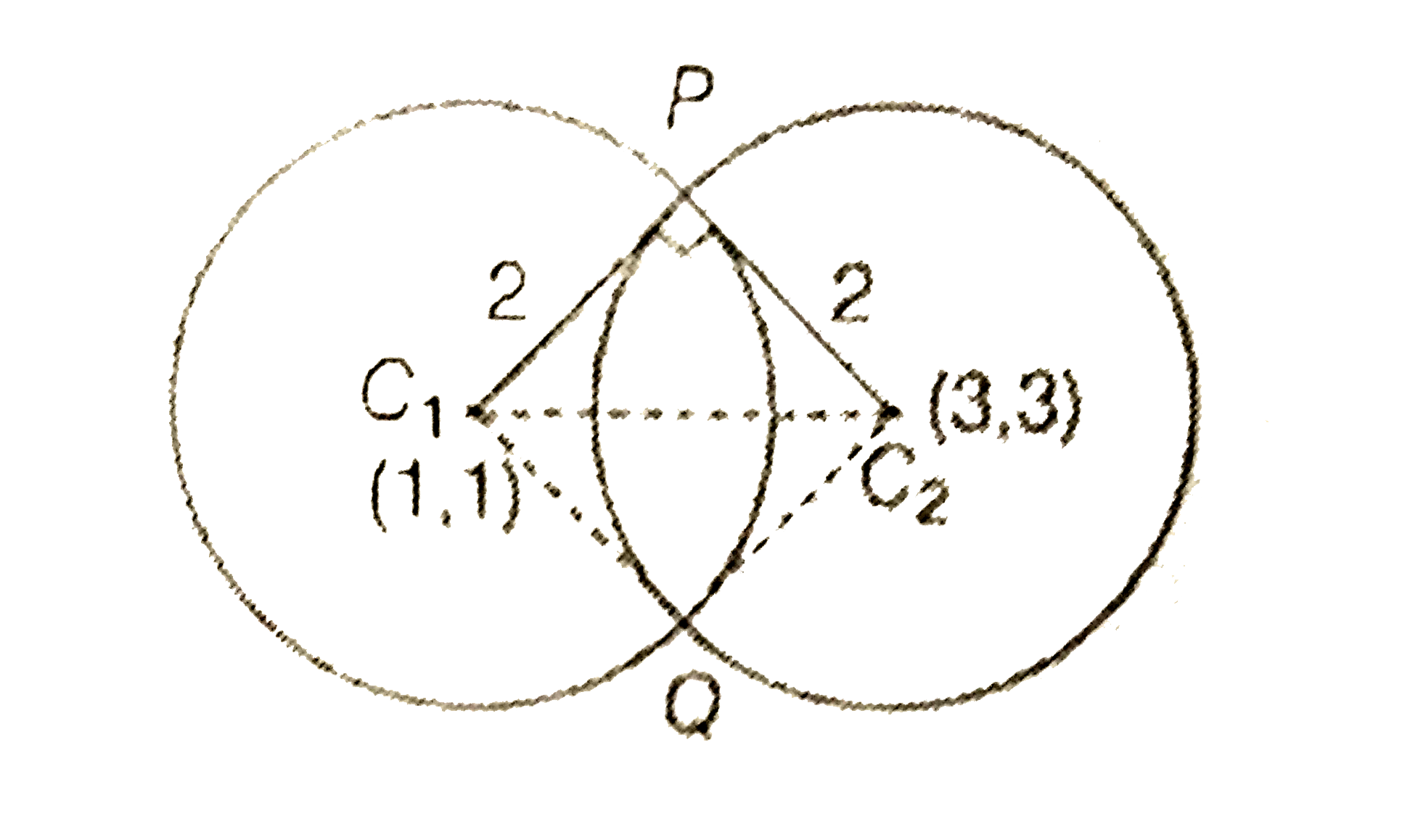A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let C(1) " and" C(2) be the centres of the circles x^(2)+y^(2)-2x-2y-2...
Text Solution
|
- Let C1 and C2 be two circles whose equations are x^2+y^2-2x=0 and x^2+...
Text Solution
|
- Consider circles C(1): x^(2) +y^(2) +2x - 2y +p = 0 C(2): x^(2) +y...
Text Solution
|
- Consider three circles C(1), C(2) and C(3) as given below: C(1) : x...
Text Solution
|
- Let C(1) and C(2) denote the centres of the circles x^(2) +y^(2)...
Text Solution
|
- The radical centre of the circles x^2+y^2-4x-6y+5=0, x^2+y^2-2...
Text Solution
|
- If C(1) and C(2) are the centres of similitude with respect to the cir...
Text Solution
|
- If the circles (x-3)^(2)+(y-4)^(4)=16 and (x-7)^(2)+y-7)^(2)=9 interse...
Text Solution
|
- Let C(1) and C(2) be the circles x^(2) + y^(2) - 2x - 2y - 2 = 0 and ...
Text Solution
|