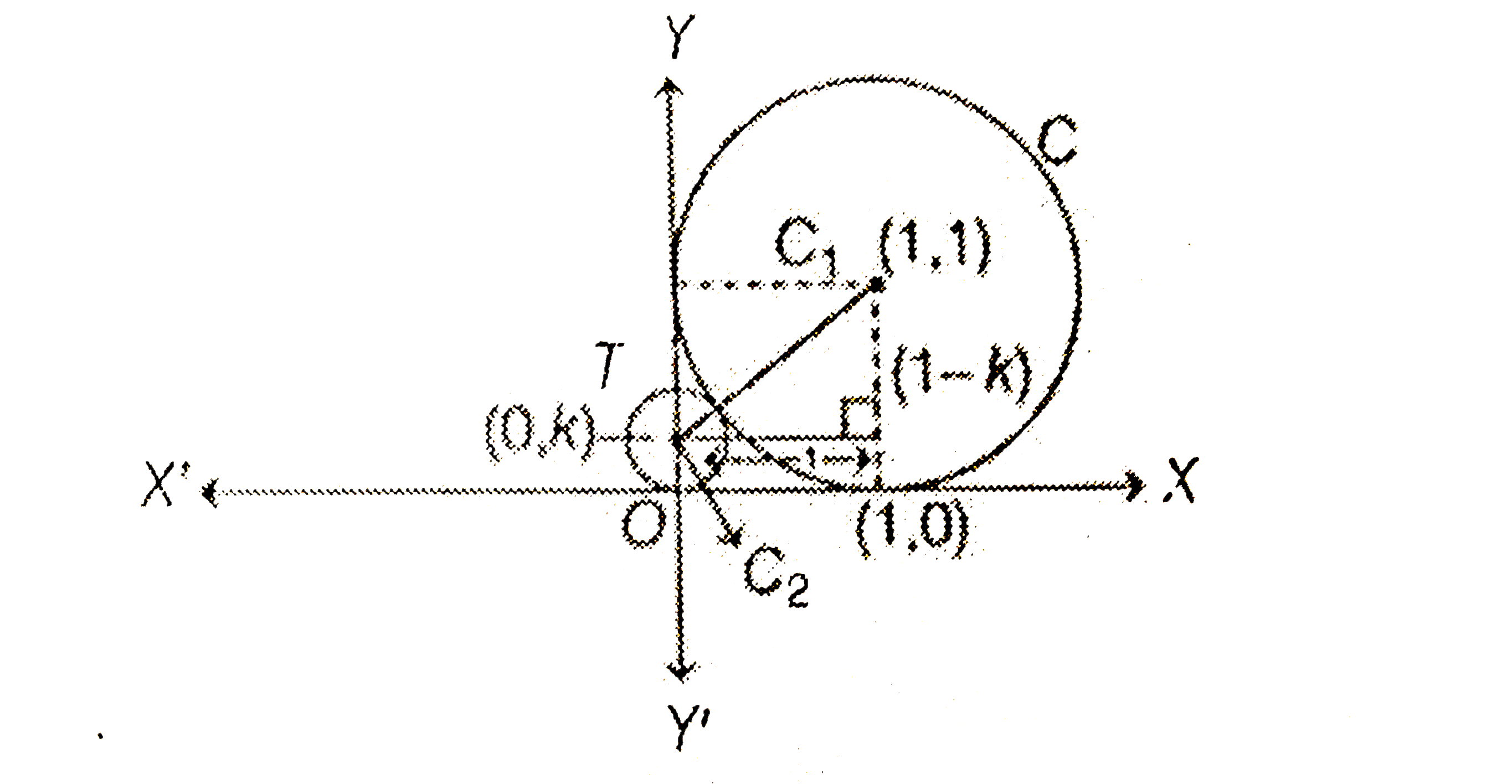A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let C be the circle with centre at (1,1) and radius =1 . If T is the ...
Text Solution
|
- Let C be the circle with centre at (1, 1) and radius = 1. If T is t...
Text Solution
|
- 1) 1/5 2) 10 3) 10v2 4) 5v2 Let C be the circle with centre at (1,1) a...
Text Solution
|
- Let C be the circle with centre at (1, 1) and radius 1 If Tis the circ...
Text Solution
|
- Let C be the circle with centre (1,1) and radius 1.If T is the circle ...
Text Solution
|
- Let be the circle with centre at (1 , 1) and radius is 1 unit . It ...
Text Solution
|
- Let C be the circle with centre at (1,1) and radius =1 . If T is the ...
Text Solution
|
- Let C be the circle with centr at (1,1) and radius =1. If T is the cir...
Text Solution
|
- माना C एक वृत्त है जिसका केंद्र (1,1) पर है तथा त्रिज्या =1 है । यदि T...
Text Solution
|