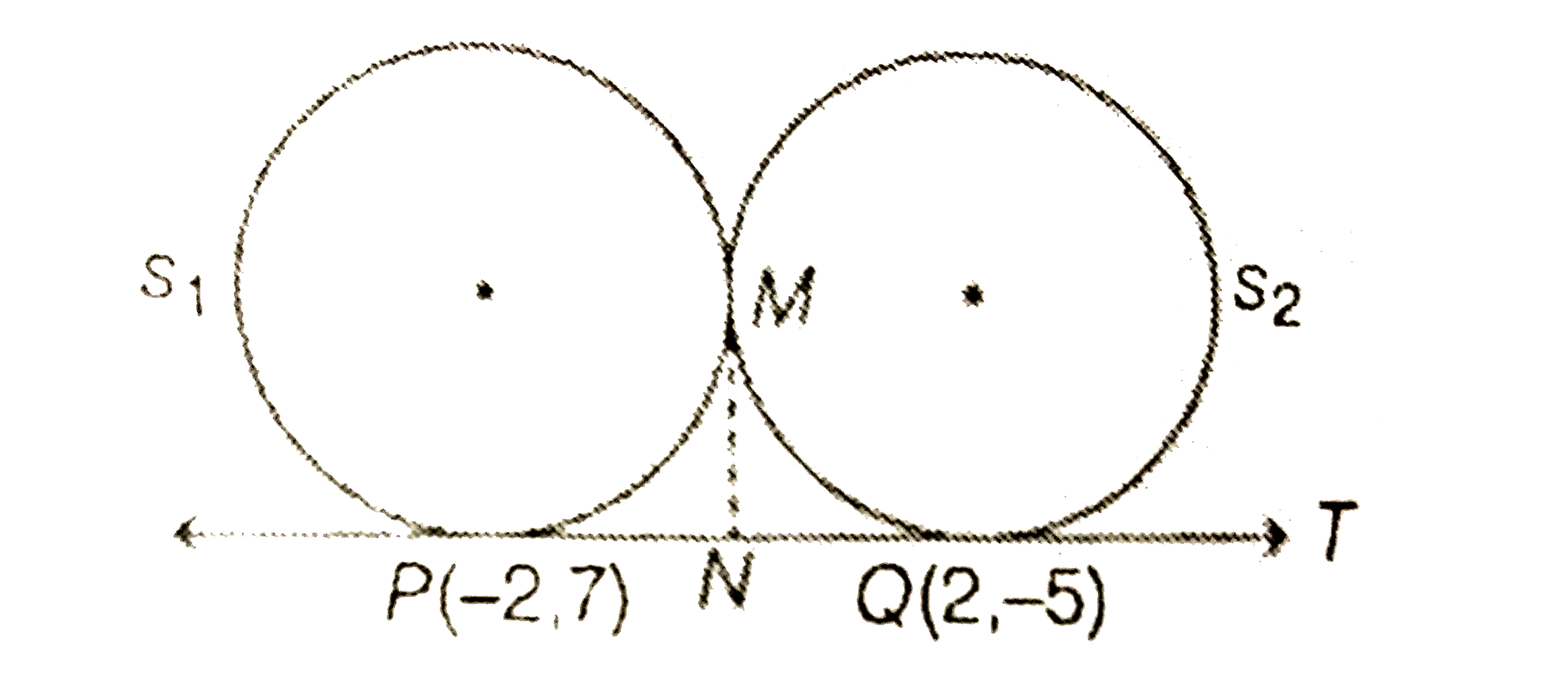A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- Let T be the line passing through the points through the points P(-2,7...
Text Solution
|
- Let S(1) and S(2) be circle passing through (2,3) and touching the coo...
Text Solution
|
- Let S(1) and S(2) be circle passing through (2,3) and touching the coo...
Text Solution
|
- Let each of the circles S(1)-=x^(2)+y^(2)+4y-1=0 S(1)-= x^(2)+y^(2...
Text Solution
|
- Let T be the line passing through the points P(-2, 7) and Q(2, -5). Le...
Text Solution
|
- Let each of the circles, S(1)=x^(2)+y^(2)+4y-1=0, S(2)=x^(2)+y^(2)...
Text Solution
|
- Let each of the circles, S(1)=x^(2)+y^(2)+4y-1=0, S(2)=x^(2)+y^(2)...
Text Solution
|
- If P is a point on the hyperbola 16x^(2) - 9y^(2) = 144 whose foci ar...
Text Solution
|
- Let T be the line passing the points P(–2, 7) and Q(2,–5). Let F(1) be...
Text Solution
|