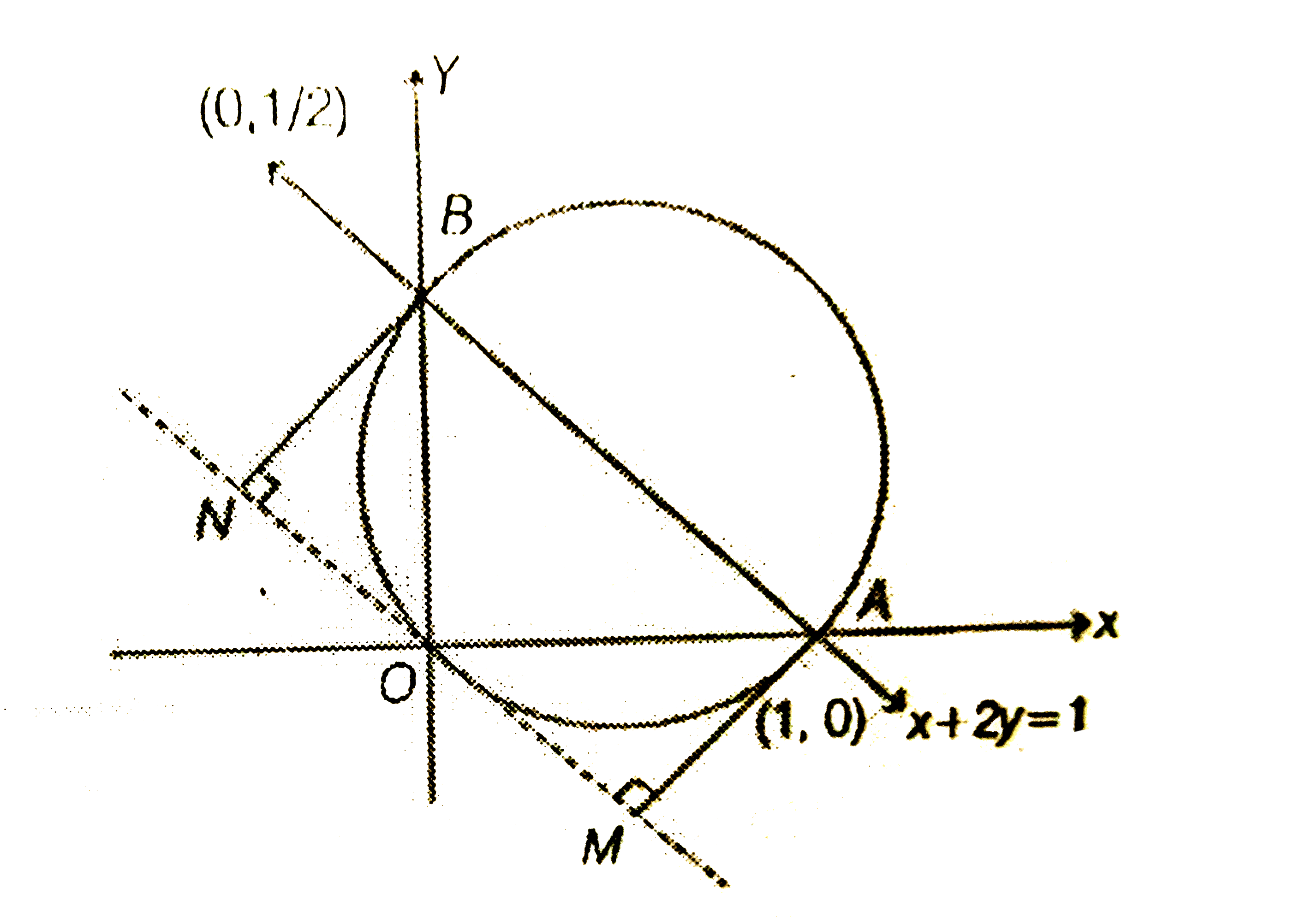A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The straight line x+2y=1 meets the coordinate axes at A and B. A circl...
Text Solution
|
- The straight line x + 2y = 1 meets the coordinate axes at A and B. A c...
Text Solution
|
- The locus of the centre of the circle passing through the origin O an...
Text Solution
|
- A line meets the coordinate axes at A and B. A circle is circumscribed...
Text Solution
|
- A line is at a distance ' c ' from origin and meets axes in A and B .T...
Text Solution
|
- A line is at a constant distance c from the origin and meets the coord...
Text Solution
|
- A line meets coordinate axes in A and B. A circle is circumscribed ab...
Text Solution
|
- A straight line x+2y=1 cuts the x and y axis at A and B.A circle passe...
Text Solution
|
- A line is at a distance c from origin and meets axes in A an dB. The l...
Text Solution
|