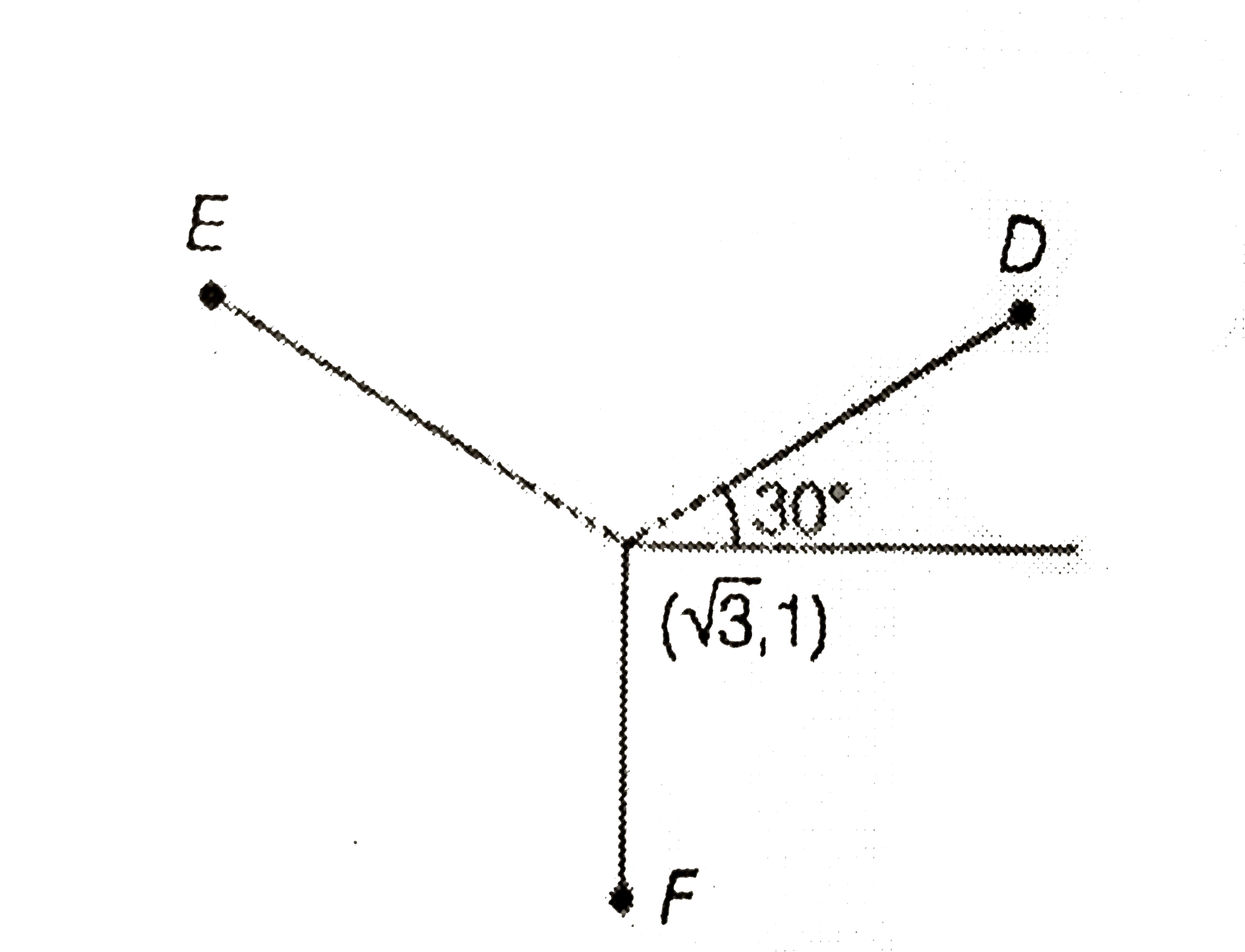
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
Text Solution
|
- A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
Text Solution
|
- A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
Text Solution
|
- A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
Text Solution
|
- समबाहु त्रिभुज PQR के अंतनिर्हित एक वृत C स्थित है जिसकी त्रिज्या 1 है...
Text Solution
|
- एक वृत्त जिसकी त्रिज्या 1 है। समबाहु त्रिभुज PQR के अन्दर स्थित है। भु...
Text Solution
|
- समबाहु त्रिभुज PQR के अंतनिर्हित एक वृत C स्थित है जिकी त्रिज्या 1 है।...
Text Solution
|
- A circle whose radius is 1. The equilateral triangle is located inside...
Text Solution
|
- A circle whose radius is 1. The equilateral triangle is located inside...
Text Solution
|