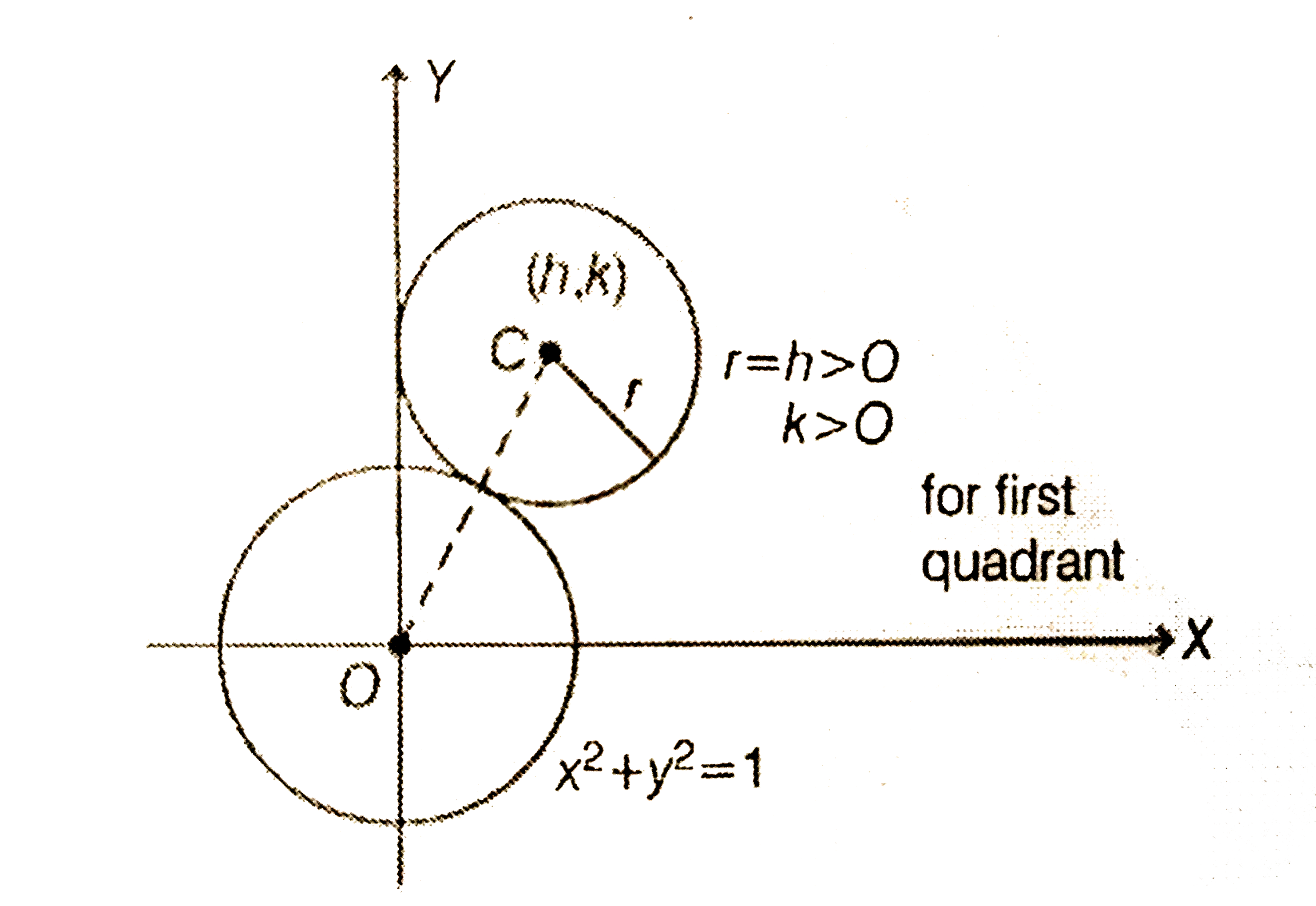A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The locus of the centres of the circles, which touch the circle, x^(2...
Text Solution
|
- The locus of centre of circle which touches the circle x^(2)+y^(2)=1 a...
Text Solution
|
- The locus of the centres of the circles which touch the circle x^(2)+y...
Text Solution
|
- The locus of the centres of the circles, which touch the circle, x^(2...
Text Solution
|
- The locus of the centres of circles which touches (y-1)^(2)+x^(2)=1 ex...
Text Solution
|
- The locus of the centre of the circle which moves such that it touches...
Text Solution
|
- The centres of those circles which touch the circle, x^(2)+y^(2)-8x-8y...
Text Solution
|
- ऐसे वृत्तों, जो वृत्त x^(2) + y^(2)=1 को बाह्रा स्पर्श करते है, Y- अक्...
Text Solution
|
- If a variable circle 'C' touches the x-axis and touches the circle x^2...
Text Solution
|