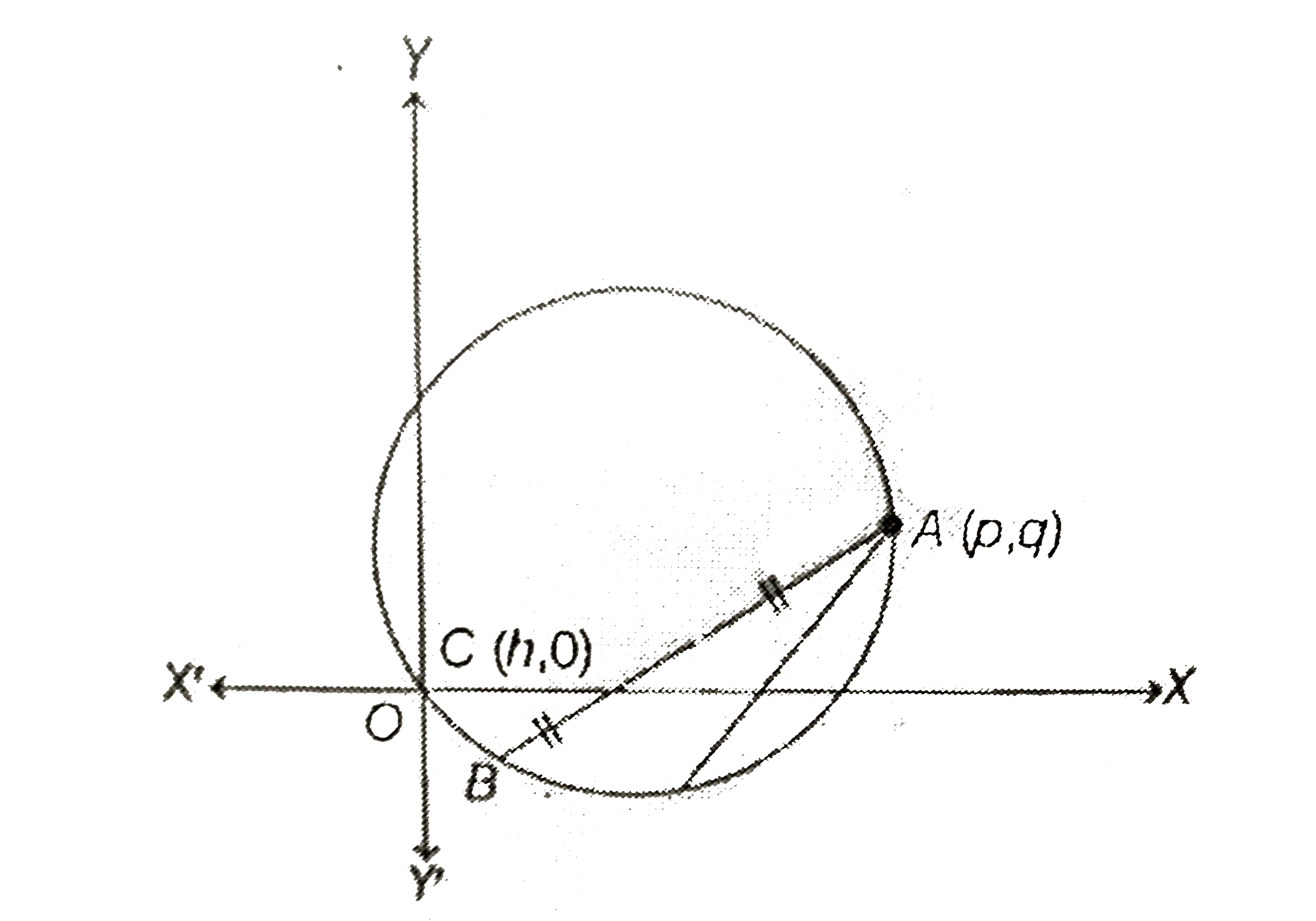A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If two distinct chords, drawn from the point (p, q) on the circle x^2+...
Text Solution
|
- If sec alpha and alpha are the roots of x^2-p x+q=0, then (a) p^2=...
Text Solution
|
- If two distinct chords,drawn from the point (p, q) on the circle x^(2)...
Text Solution
|
- Solve for x and y:(q)/(p)x+(p)/(q)y=p^(2)+q^(2);x+y=2pq
Text Solution
|
- p(x+y) +q(x-y) =p^(2) -pq +q^(2) और p(x+y) -q (x-y) =p^(2) +pq +q^(2)...
Text Solution
|
- If two distinct chords, drawn from the point (p,q) on the circle x^(2)...
Text Solution
|
- If sec alpha and alpha are the roots of x^2-p x+q=0, then (a) p^2=...
Text Solution
|
- If two distinct chords, drawn from the point (p, q) on the circle x^2+...
Text Solution
|
- यदि p तथा q भिन्न वास्तविक संख्याये है, तो 2{(x-p)(x-q)+(p-x)(p-q)+(q-...
Text Solution
|