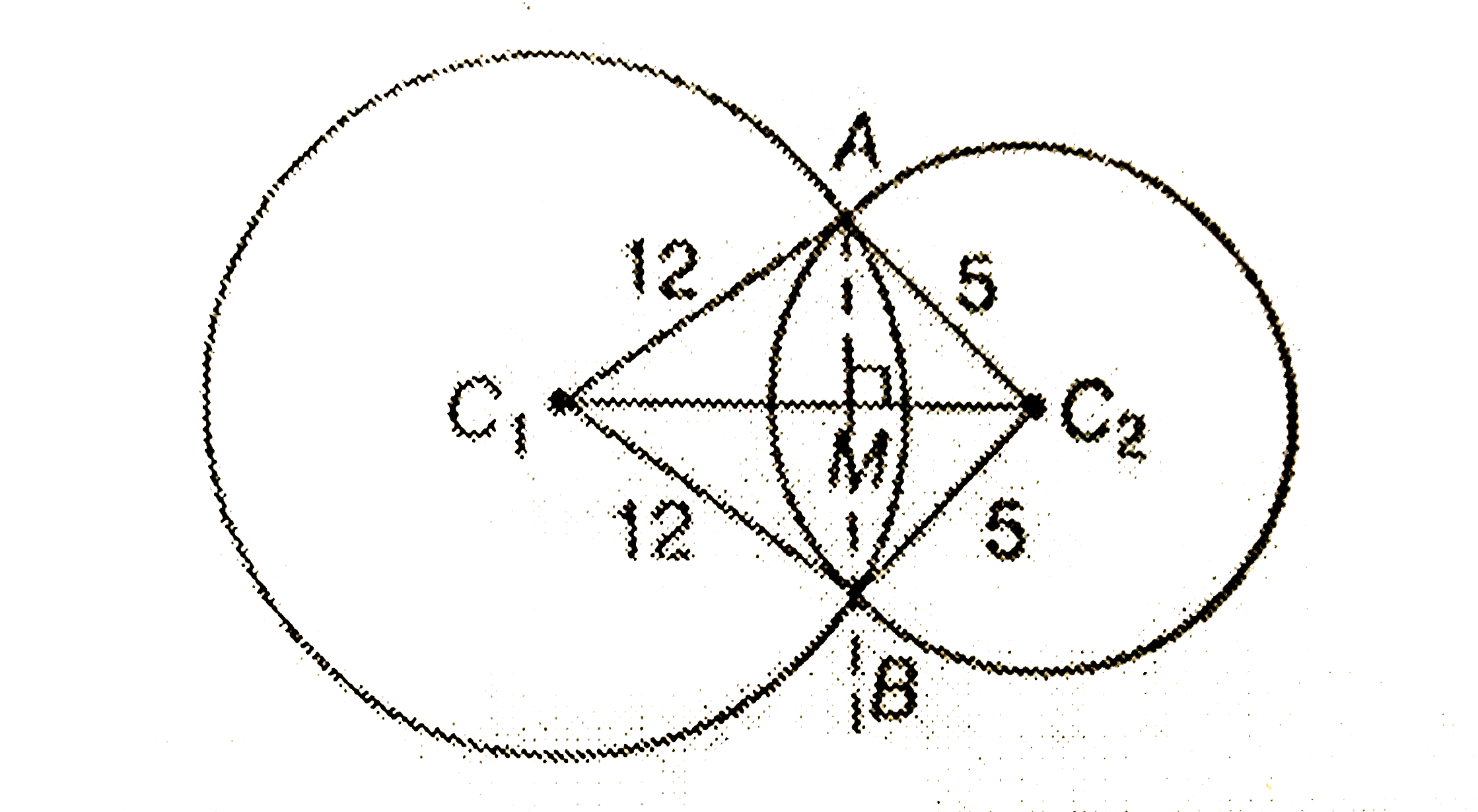A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- If the angle of intersection at a point where the two circles with ra...
Text Solution
|
- If the angle of intersection at a point where the two circles with ra...
Text Solution
|
- 5 सेमी तथा 3 सेमी त्रिज्या वाले दो वृत्त दो बिन्दुओ पर प्रतिच्छेद करते...
Text Solution
|
- 5 सेमि और 3 सेमि त्रिज्या वाले दो वृत्त, दो बिन्दुओं पर प्रतिच्छेद करत...
Text Solution
|
- 10 सेमी तथा 8 सेमी त्रिज्या वाले दो वृत्त प्रतिच्छेद करते है। इनकी उभ...
Text Solution
|
- Two circles of radii 5 cm and 3 cm intersect at two points and the dis...
Text Solution
|
- Two circles of radii 5 cm and 3 cm intersect at two points and the dis...
Text Solution
|
- यदि एक बिंदु जहाँ 5cm तथा 12cm त्रिज्या के दो वृत्त एक दूसरे को 90^(@)...
Text Solution
|
- Two circles whose radii are 10 cm and 8 cm respectively, intersect eac...
Text Solution
|