A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The locus of the middle point of the chord of contact of tangents draw...
Text Solution
|
- The locus of the middle point of the chord of contact of tangents draw...
Text Solution
|
- The locus of the mid-point of the chord of contact of tangents drawn f...
Text Solution
|
- Tangent are drawn from the point (3, 2) to the ellipse x^2+4y^2=9 ....
Text Solution
|
- Find the locus of the middle points of the chords of contact of tangen...
Text Solution
|
- Tangents are drawn to a unit circle with centre at the origin from eac...
Text Solution
|
- The locus of the mid-point of the chord of contact of tangents drawn f...
Text Solution
|
- The locus of the mid-point of the chord of contact of tangents drawn f...
Text Solution
|
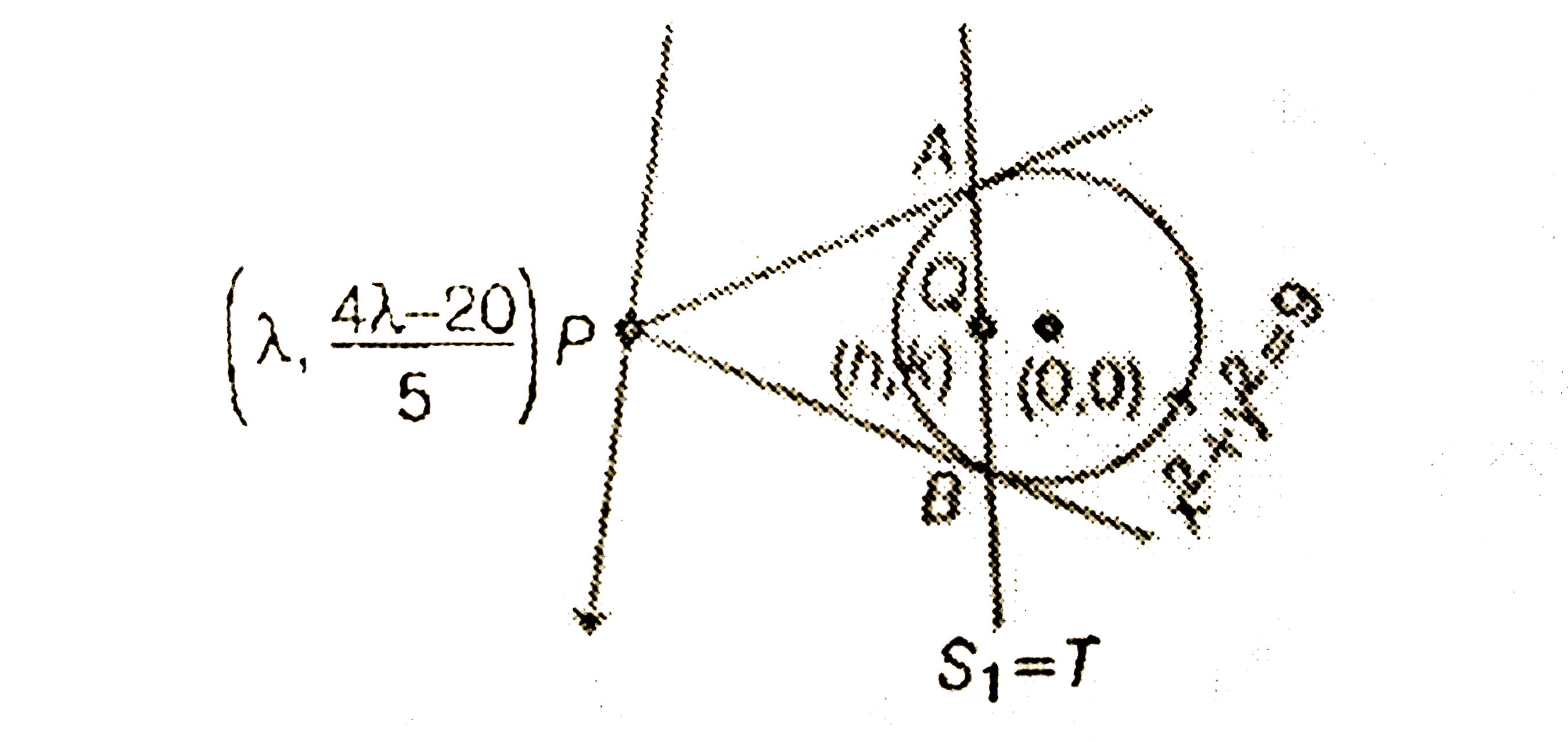
- सरल रेखा 4x-5y=20 के बिंदुओं से वृत्त x^(2)+y^(2)=9 पर डाली गई स्पर्श ...
Text Solution
|