A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
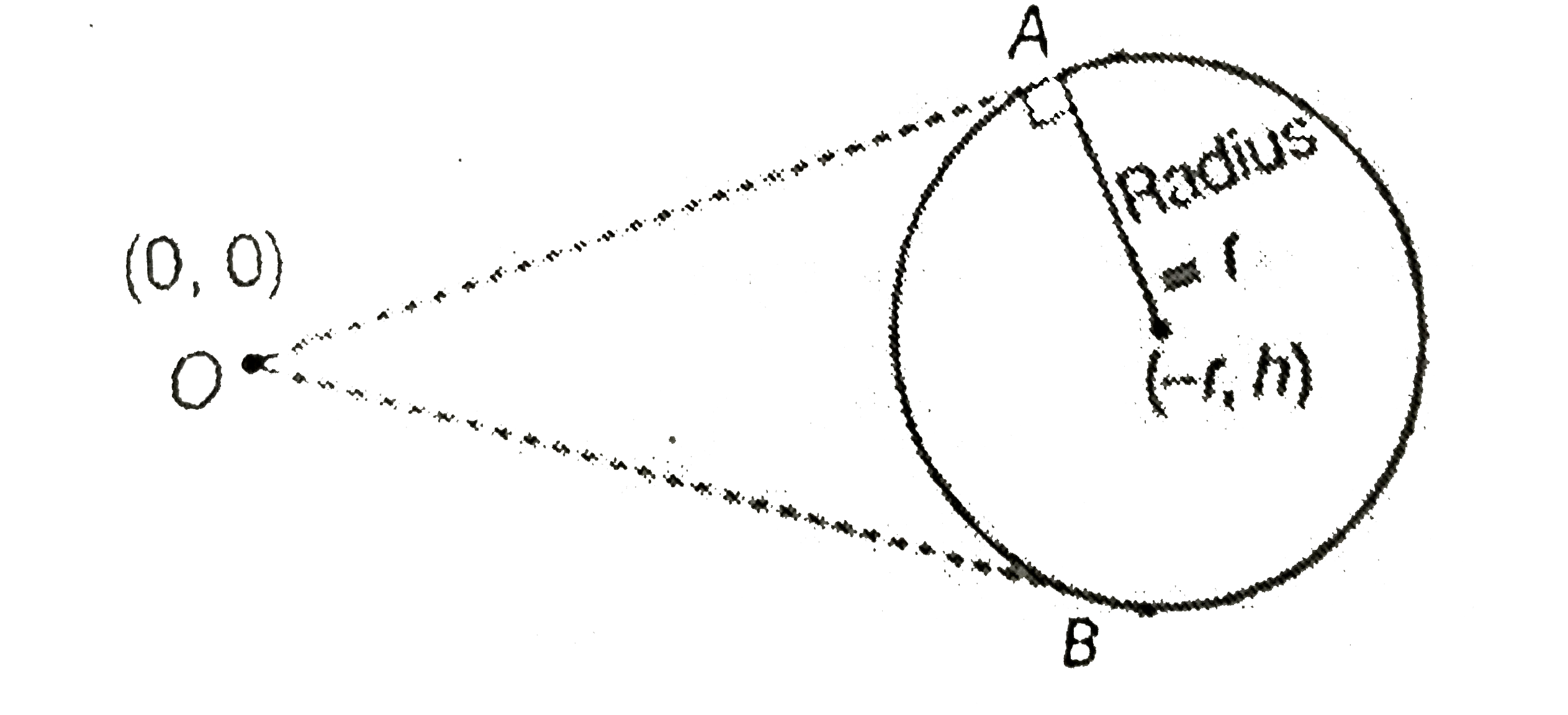
- The equation of the tangents drawn from the origin to the circle x^(2)...
Text Solution
|
- The equation of tangents drawn from the origin to the circlex^2+y^2-2r...
Text Solution
|
- The tangents drawn from the origin x^(2)+y^(2)-2rx-2hy+h^(2)=0 are per...
Text Solution
|
- The tangents drawn from the origin to the circle x^2+y^2-2rx-2hy+h^2=0...
Text Solution
|
- मूल बिन्दु से वृत्त x^2+y^2 -2rx-2hy+h^2=0 पर खींची गई स्पर्शियों का स...
Text Solution
|
- The equations of tangents drawn from the origin to the circle x^2+y^2-...
Text Solution
|
- News x^(2) + y^(2) - 2rx - 2hy + h^(2) = 0 But the equation of tangent...
Text Solution
|
- Show that the equations of the tangents drawn from the origin to the c...
Text Solution
|
- The equation of tangents drawn from the origin to the circlex^2+y^2-2r...
Text Solution
|