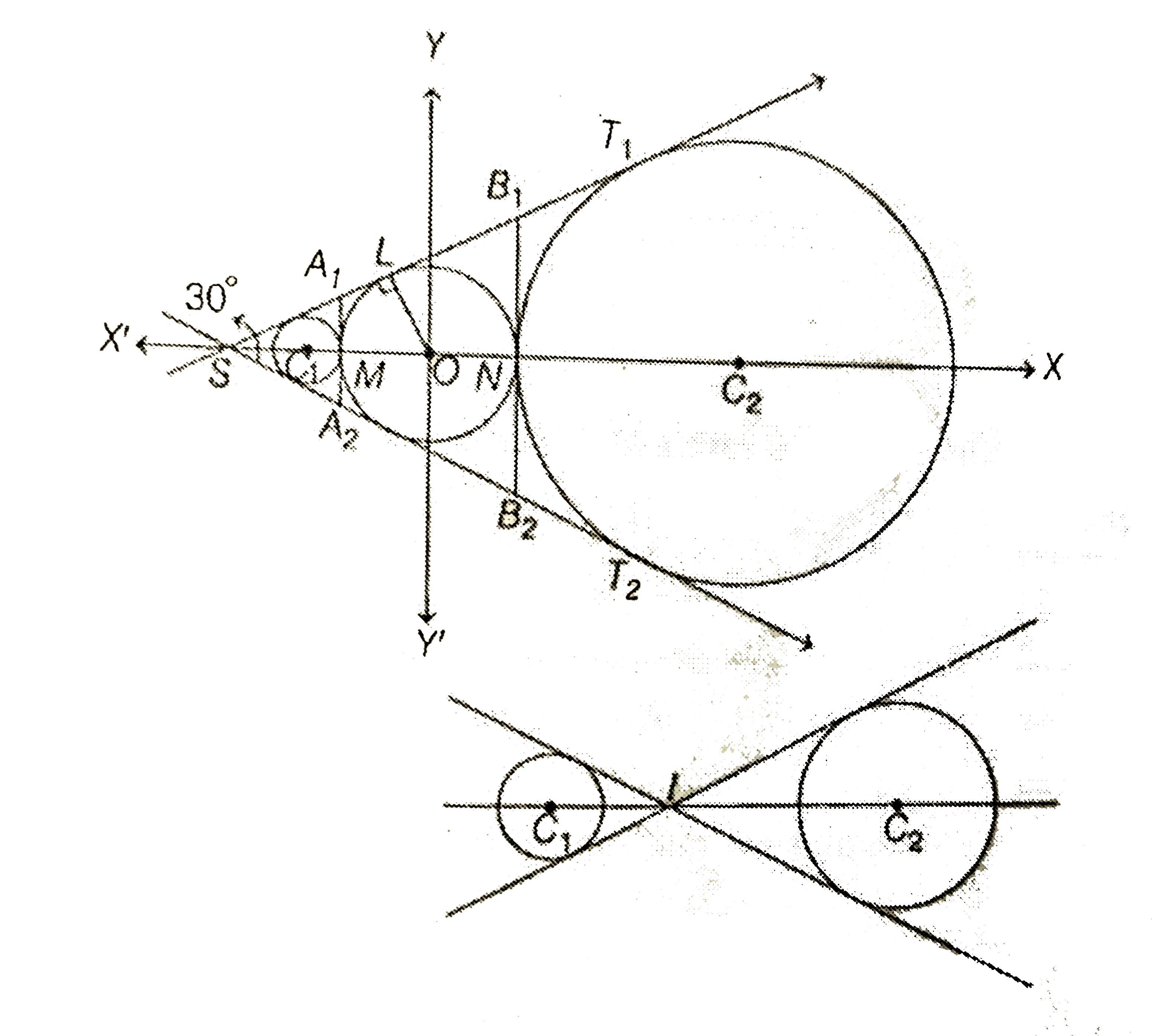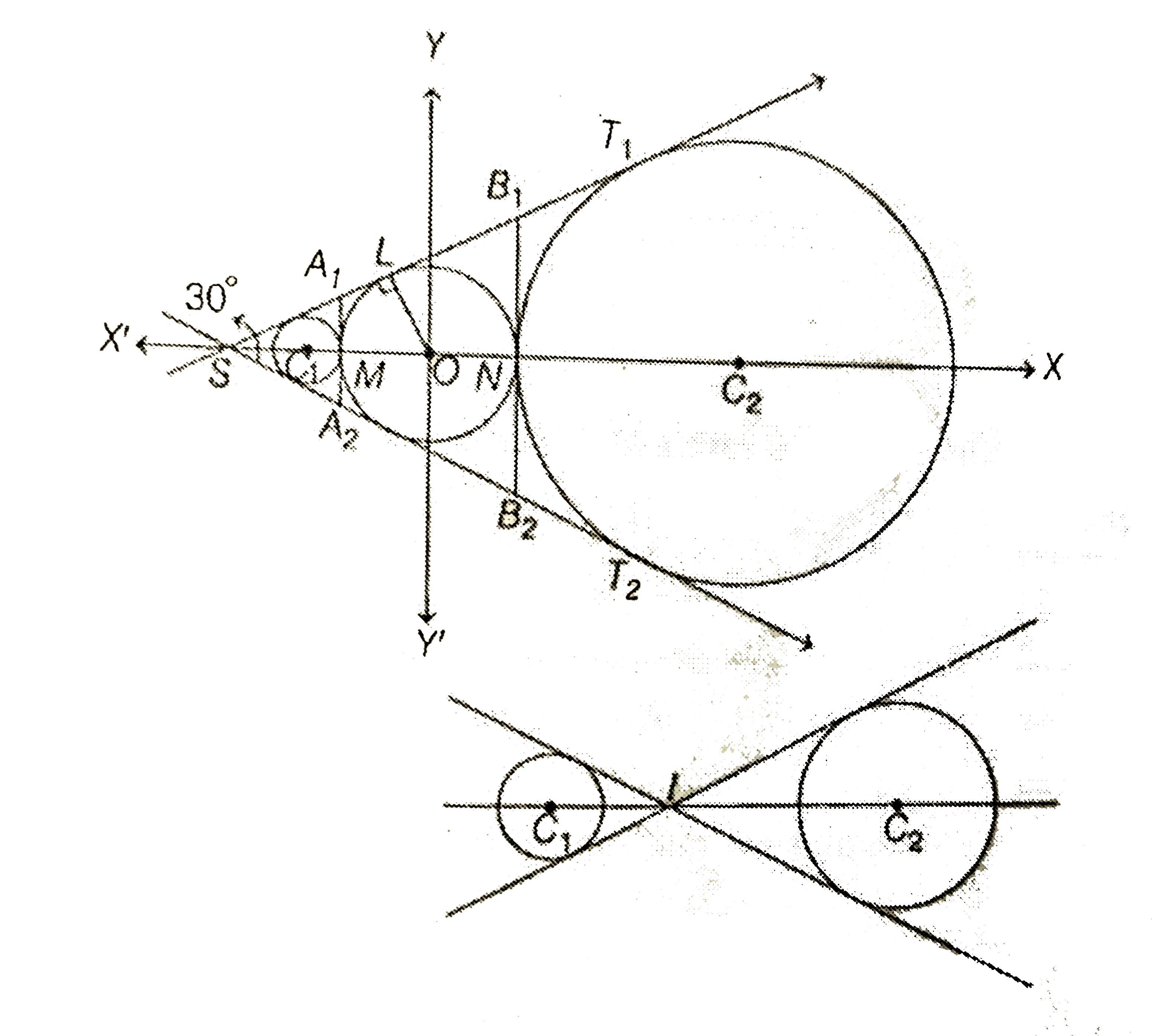
From figure it is clear that, `Delta OLS` is clear that, `DeltaOLS` is a right triangle with right angle at L.
Also, OL = 1 and OS = 2
`therefore 1 sin (angleLSO)=(1)/(2)rArr angleLSO=30^(@)`
Since,`SA_(1)= S_(2), Delta SA_(1)A_(2)` is an equilateral triangle.
the circle with centre at `C_(1)` is a circle insribed in the `Delta SA_(1)A_(2)`. Therefore centre `C_(1)` is a circle inscribed of `DeltaSA_(1)A_(2)`. This `C_(1)` divides SM in the ratio `2:1`. therefore coordinates of `C_(1)` are `(-4//3,0)` and its radius `= C_(1)M=1//3`
`therefore` Its equation is `(x+4//3)^(2)+y^(2)=(1//3)^(2)" "...(i)`
The other cirlce touches the equilateral triangle `SB_(1)A_(2)`.
externally. Its radius r is given by `r=(Delta)/(s-a)`
where `B_(1)B_(2)=a "But" Delta = (1)/2)(a)(SN)=(3)/(2)a`
and `s-a=(3)/(2)a-a=(a)/(2)`
Thus, r = 3
`rArr " Coordinates of " C_(2) " are " (4, 0)`.
`therefore` Equation of circle with centre at `C_(2)` is
`(x-4)^(2)+y^(2)=3^(2)" "...(ii)`
EQuation of common tangents to circle (i) and circle C are
`x = -1 and y=pm(1)/(sqrt3)(x+2)" "[T_(1) and T_(2)]`
Equation of common tangents to circle (ii) and circle C are
`x=1and y=pm(1)/(sqrt3)(x+2)" "...[T_(1)and T_(2)]`
Two tangents common to (i) and (ii) ar `T_(1) and T_(2)` at O. To find the remaining two trasnverse tangents to (i) and (ii), we find a point I which divides the joint of `C_(1) C_(2)` in the ratio `r_(1) : r_(2)=1//3:3 = 1 : 9 `
Therefore, coordintates of I are `(-4//5, 0)`
Equation of any line through I is `y = m (x+4//5)`. It will touch (i) if
`|m((-4)/(3)+(4)/(5))-0|/(sqrt(1+m^(2)))=(1)/(3)rArr|-(8m)/(15)|=(1)/(3)sqrt(1+m^
(2))`
`rArr 64m^(2)=25(1+m^(2))`
`rArr 39m^(2)=25rArrm=pm(5)/(sqrt39)`
Therefore, these tangents are `y = pm (5)/(sqrt39)(x+(4)/(5))`