Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- C(1) and C(2) are two concentric circles, the radius of C(2) being tw...
Text Solution
|
- Transverse common tangents are drawn from O to the two circles C(1),C(...
Text Solution
|
- Prove that (C(0)+C(1))(C(1)+C(2))(C(2)+C(3))(C(n-1)+C(n))=((n+1)^(n))/...
Text Solution
|
- If C(1): x^(2)+y^(2) =(3+2sqrt(2))^(2) be a circle. PA and PB are pair...
Text Solution
|
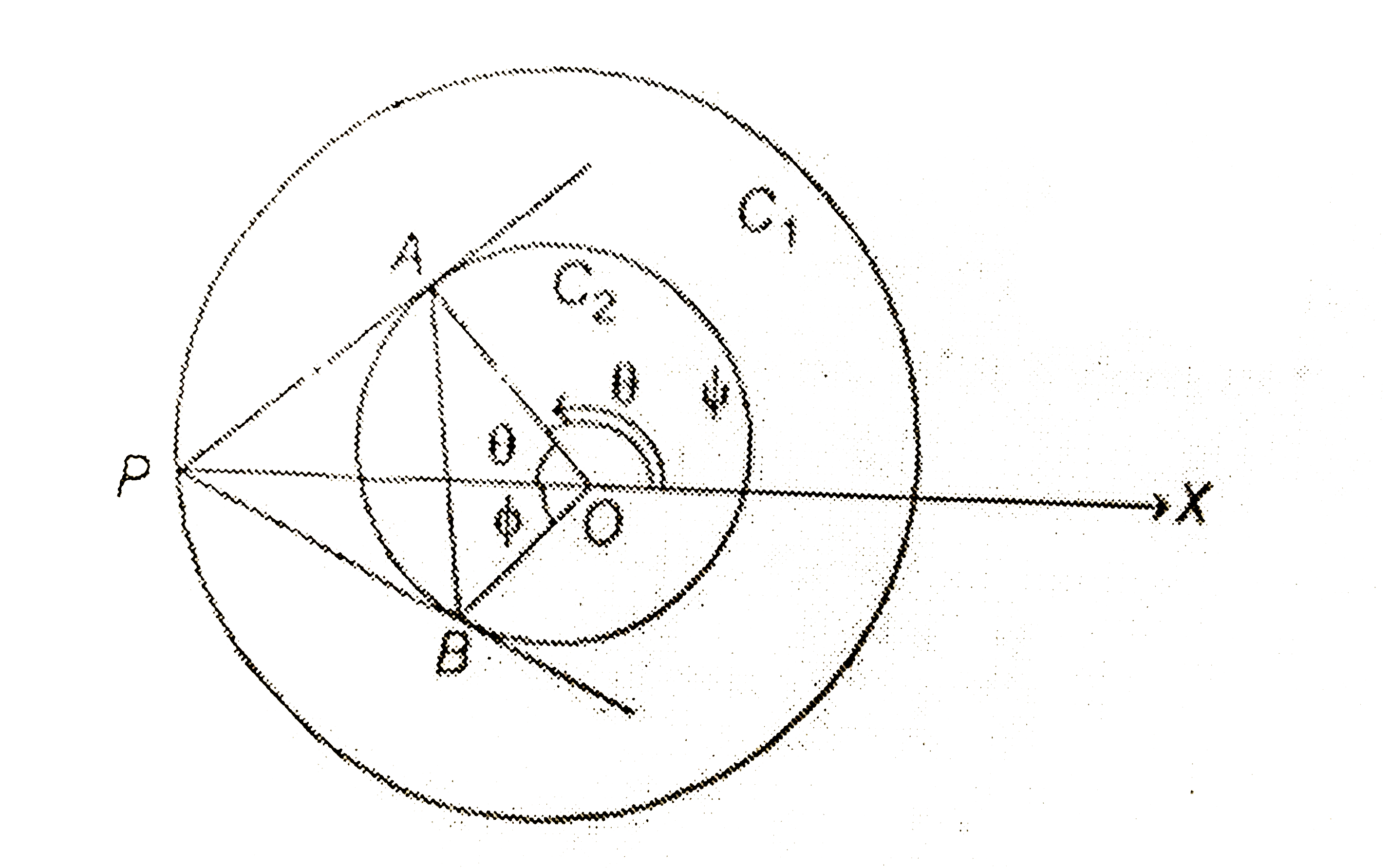
- C(1) and C(2) are two concentrate circles, the radius of C(2) being t...
Text Solution
|
- If C(1),C(2),C(3),... is a sequence of circles such that C(n+1) is the...
Text Solution
|
- Prove that : Prove that (C(1))/(C(0))+2.(C(2))/(C(1))+3.(C(3))/(C(2)...
Text Solution
|
- If C(0),C(1),C(2),…,C(n) are the binomial coefficients in the expansio...
Text Solution
|
- Consider the circle C(1):x ^(2) +y ^(2) -6x - 8y + 15=0, C(2) : x ^(2)...
Text Solution
|