Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
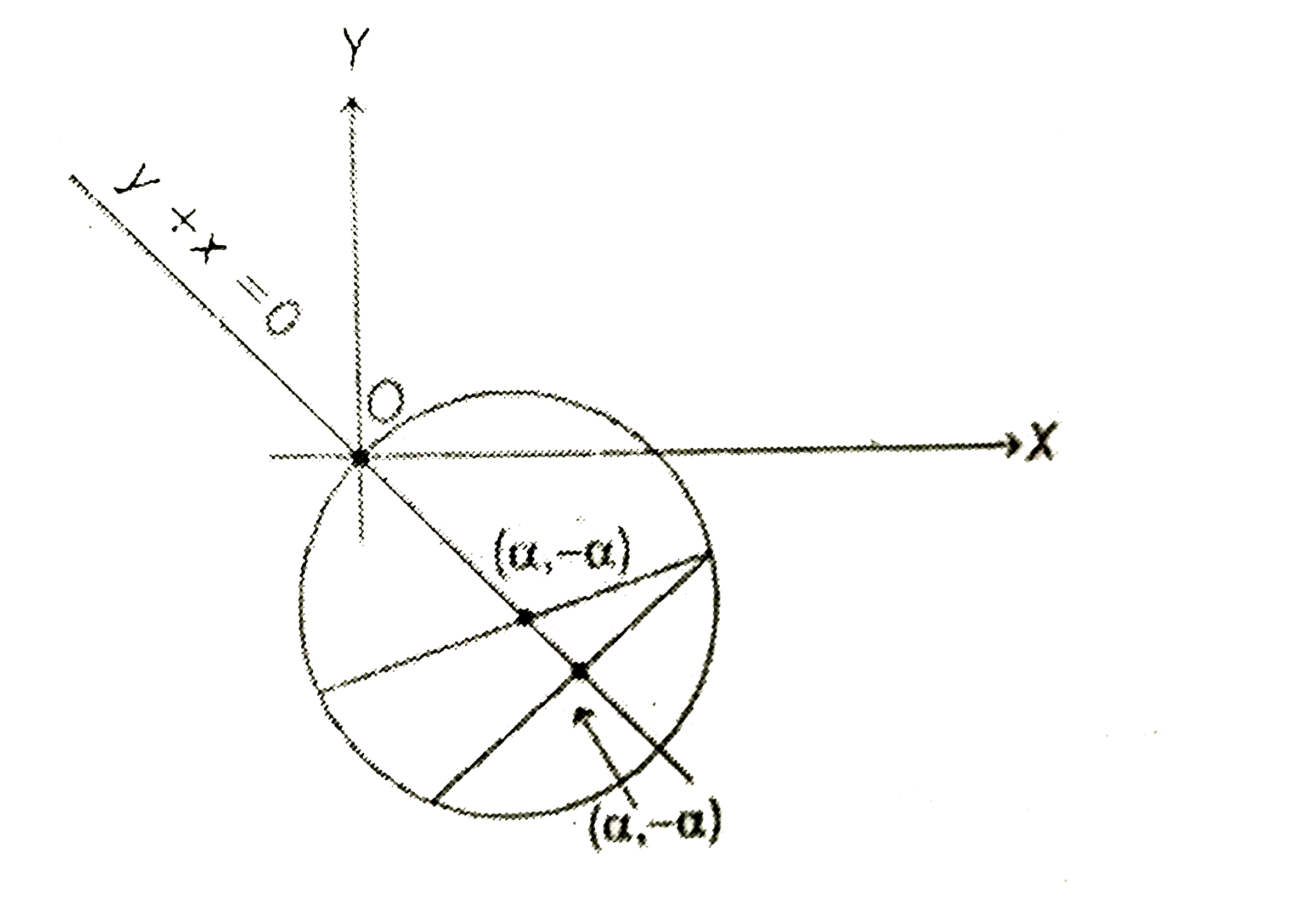
- Find the intervals of the values of a for which the line y+x=0 bisects...
Text Solution
|
- Find the equation of the normal to the circle x^2+y^2=9 at the point (...
Text Solution
|
- Find the intervals of the values of a for which the line y+x=0 bisects...
Text Solution
|
- If y=tan^(-1){(sqrt(1+x^2)+sqrt(1-x^2))/(sqrt(1+x^2)-sqrt(1-x^2))} , -...
Text Solution
|
- Tangents drawn from (2, 0) to the circle x^2 + y^2 = 1 touch the circl...
Text Solution
|
- (1) x^(2)-(sqrt(2)+1)x+sqrt(2)=0
Text Solution
|
- a के मान के लिए वे अंतराल ज्ञात कीजिए, जिसके लिए रेखा x+y=0 बिन्दु ((1...
Text Solution
|
- Identify the curve sqrt((x+1)^(2)+y^(2))+ sqrt(x^(2)+(y-1)^(2))-2 =0
Text Solution
|
- Evaluate the following limits : lim(x to 0)(sqrt(1-x^(2))-sqrt(1+x^(...
Text Solution
|