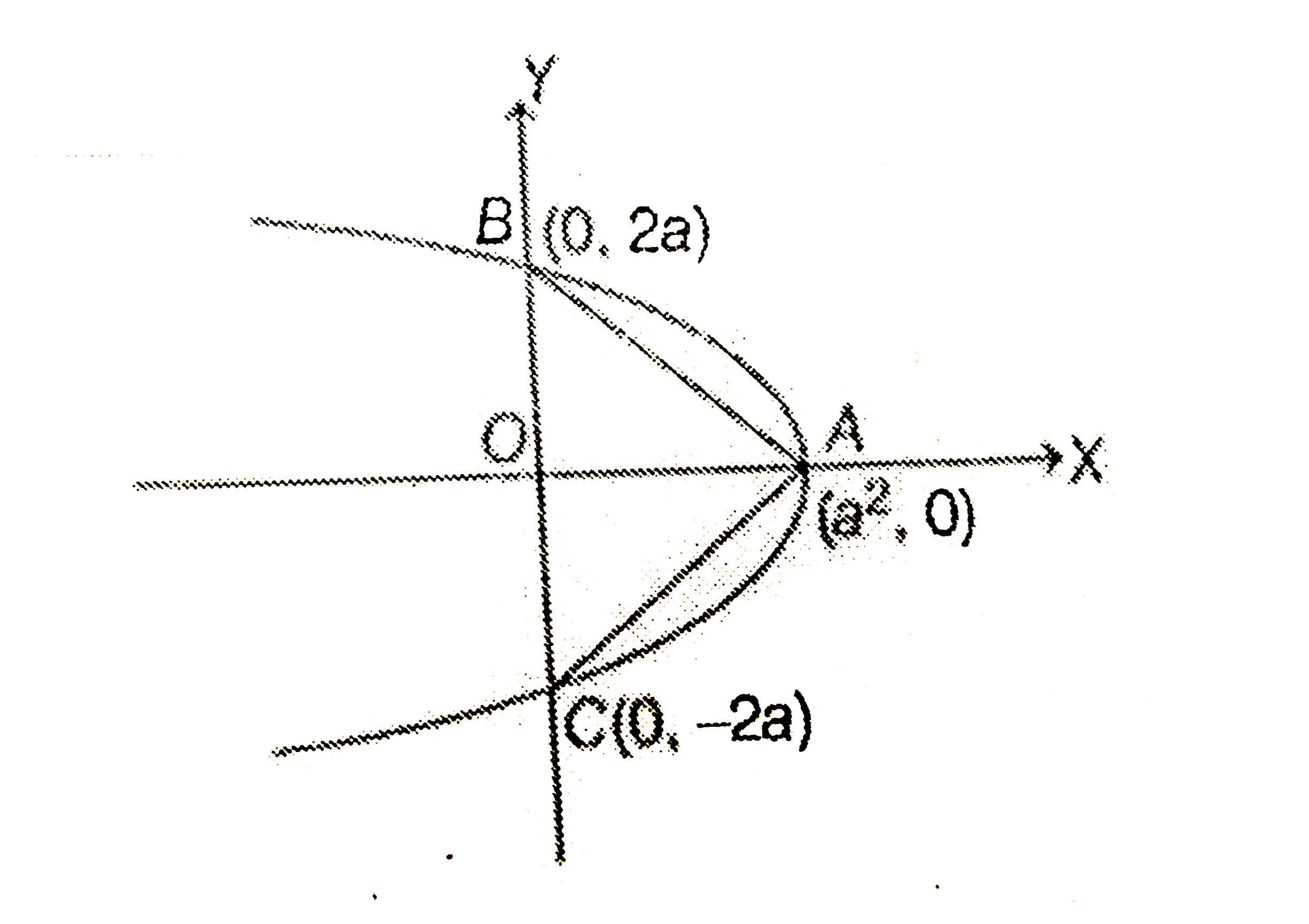
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If the area of the triangle whose one vertex is at the vertex of the p...
Text Solution
|
- Find the point on the parabola y^(2)=4ax(a>0) which forms a triangle o...
Text Solution
|
- y^2+4(x−a^2)=0. One of the vertexes of Delta'(Delta) is a vertex of...
Text Solution
|
- If the area of the triangle whose one vertex is at the vertex of the p...
Text Solution
|
- परवलय y^2=4 ax के अंतर्गत एक समबाहु त्रिभुज है जिसका एक शीर्ष परवलय क...
Text Solution
|
- An equilateral teiangle is inscribed in the parabola y^(2)=x whose one...
Text Solution
|
- An Equilateral triangle is inscribed in the parabola y^(2)=4x if one v...
Text Solution
|
- An Equilateral triangle is inscribed in the parabola y^(2)=4x if one v...
Text Solution
|
- An equailateral triangle is inscribed in the parabola y^(2)=4ax whose ...
Text Solution
|