Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
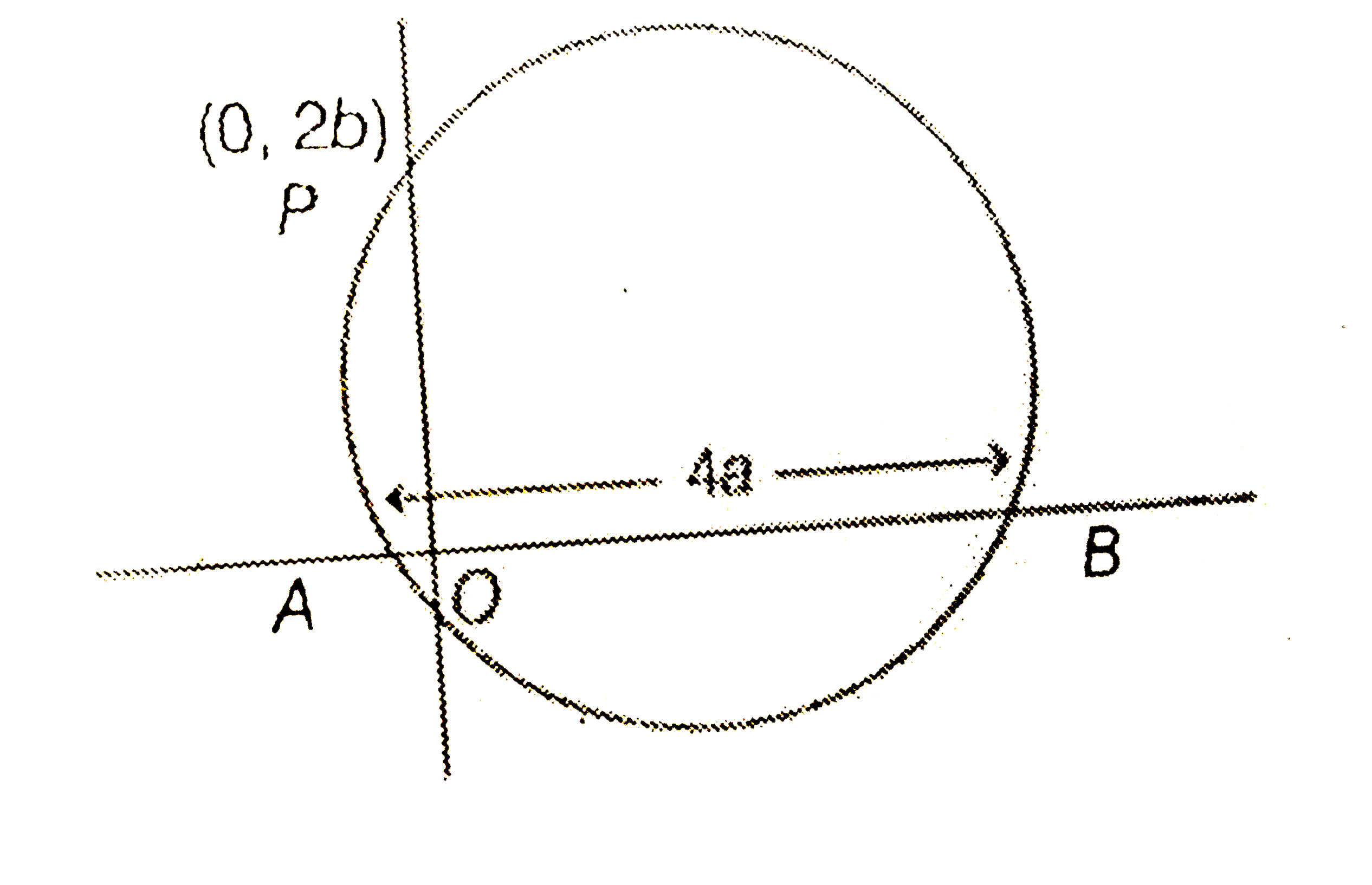
- A circle cuts a chord of length 4a on the x-axis and passes through a ...
Text Solution
|
- Prove that the locus of the center of a circle, which intercepts a cho...
Text Solution
|
- A circle cuts the chord on x-axis of length 4a. If this circle cuts th...
Text Solution
|
- If the centre of the circle passing through the origin is (3,4). th...
Text Solution
|
- सिद्ध कीजिए की उस वृत्त के केन्द्र का बिन्दुपथ जो x-अक्ष से दी हुई लम्...
Text Solution
|
- A circle is drawn to cut a chord of length 2a unit along x-axis and to...
Text Solution
|
- A circle cuts a chord of length 4a on the x-axis and passes through a ...
Text Solution
|
- Prove that the locus of the center of a circle, which intercepts a cho...
Text Solution
|
- A circle cuts the chord on x-axis of length 4a. If this circle cuts th...
Text Solution
|