Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
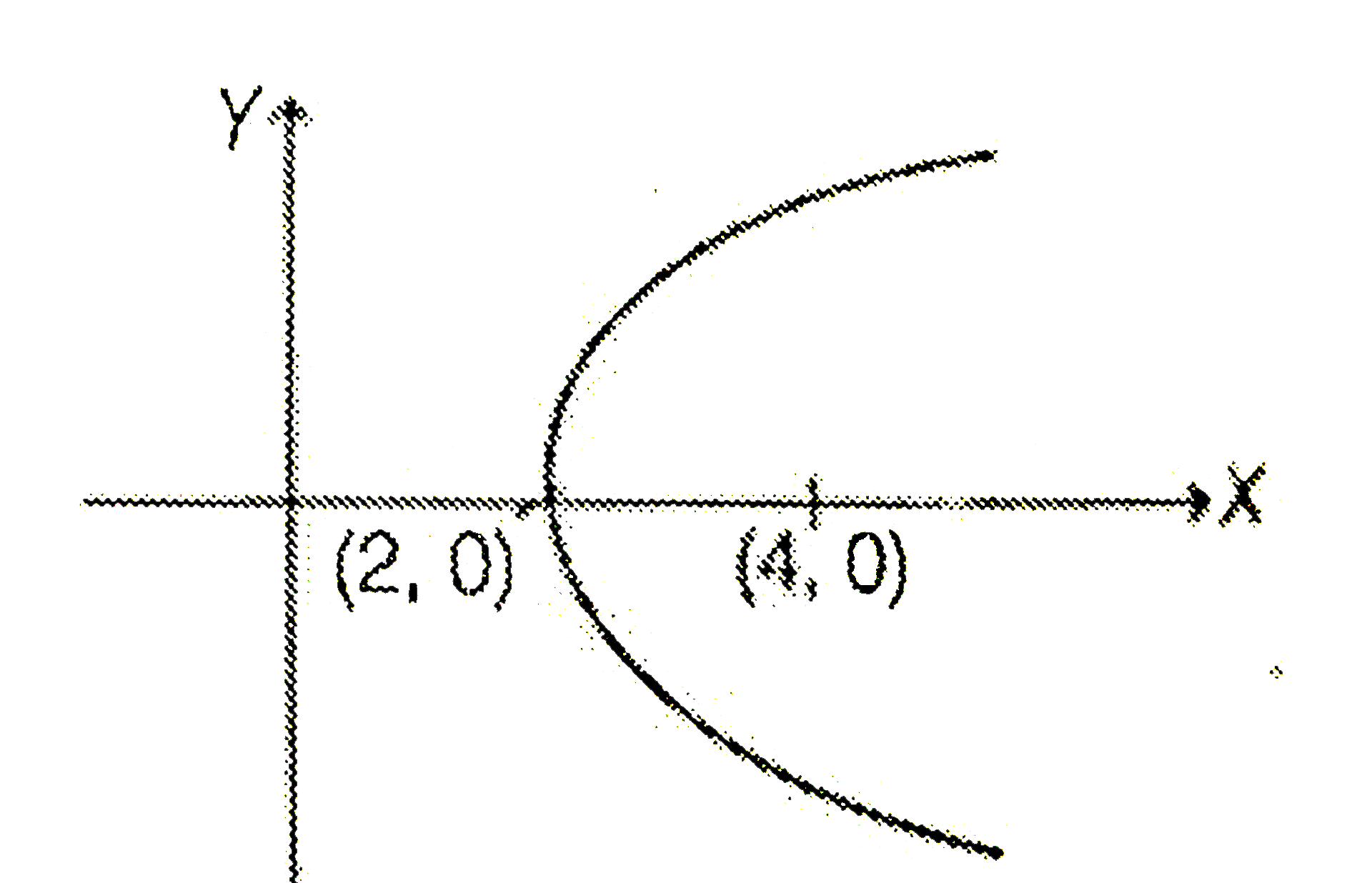
- There si a parabola having axis as x-axis, vertex is at a distance of ...
Text Solution
|
- There si a parabola having axis as x-axis, vertex is at a distance of ...
Text Solution
|
- Prove that the equation of the parabola whose vertex and focus lie on ...
Text Solution
|
- Axis of a parabola lies along x-axis. If its vertex and focus are at d...
Text Solution
|
- The equation of parabola whose vertex and focus lie on the axis of x a...
Text Solution
|
- If axis of the parabola lie along y-axis and if vertex is at a distanc...
Text Solution
|
- show that the equation of the parabola whose vertex and focus are on ...
Text Solution
|
- The vertex and focus of a parabola are at a distance of h and k units ...
Text Solution
|
- There si a parabola having axis as x-axis, vertex is at a distance of ...
Text Solution
|