Home
Class 12
MATHS
Tangent and normal are drawn at P(16,16)...

Tangent and normal are drawn at P(16,16) on the parabola `y^(2)=16x`, which intersect the axis of the parabola at A and B, espectively. If C is the centre of the circle through the points P,A and B and `angleCPB=theta`, then a value of `tantheta` is

A

`(1)/(2)`

B

2

C

3

D

`(4)/(3)`

Text Solution

Verified by Experts

The correct Answer is:
B
Equation of tangent and normal to the curve `y^(2) = 16x` at (16, 16) is `x- 2y + 16 = 0` and `2x + y - 48 = 0` respectively.

`A = (-16, 0) B = (24, 0)`
`:' C` is the centre of circle passing through PAB i.e.,
Slope of `PC = (16 - 0)/(16 - 4) = (16)/(12) = (4)/(3) = m_(1)`
Slope of `PB = (16 - 0)/(16 - 24) = (16)/(-8) = - m_(2)`
`tan theta = |(m_(1) - m_(2))/(1 + m_(1)m_(2))|`
`implies tan theta = |((4)/(3) + 2)/(1 - ((4)/(3))(2))| implies tan theta = 2`
Promotional Banner

Similar Questions

Explore conceptually related problems

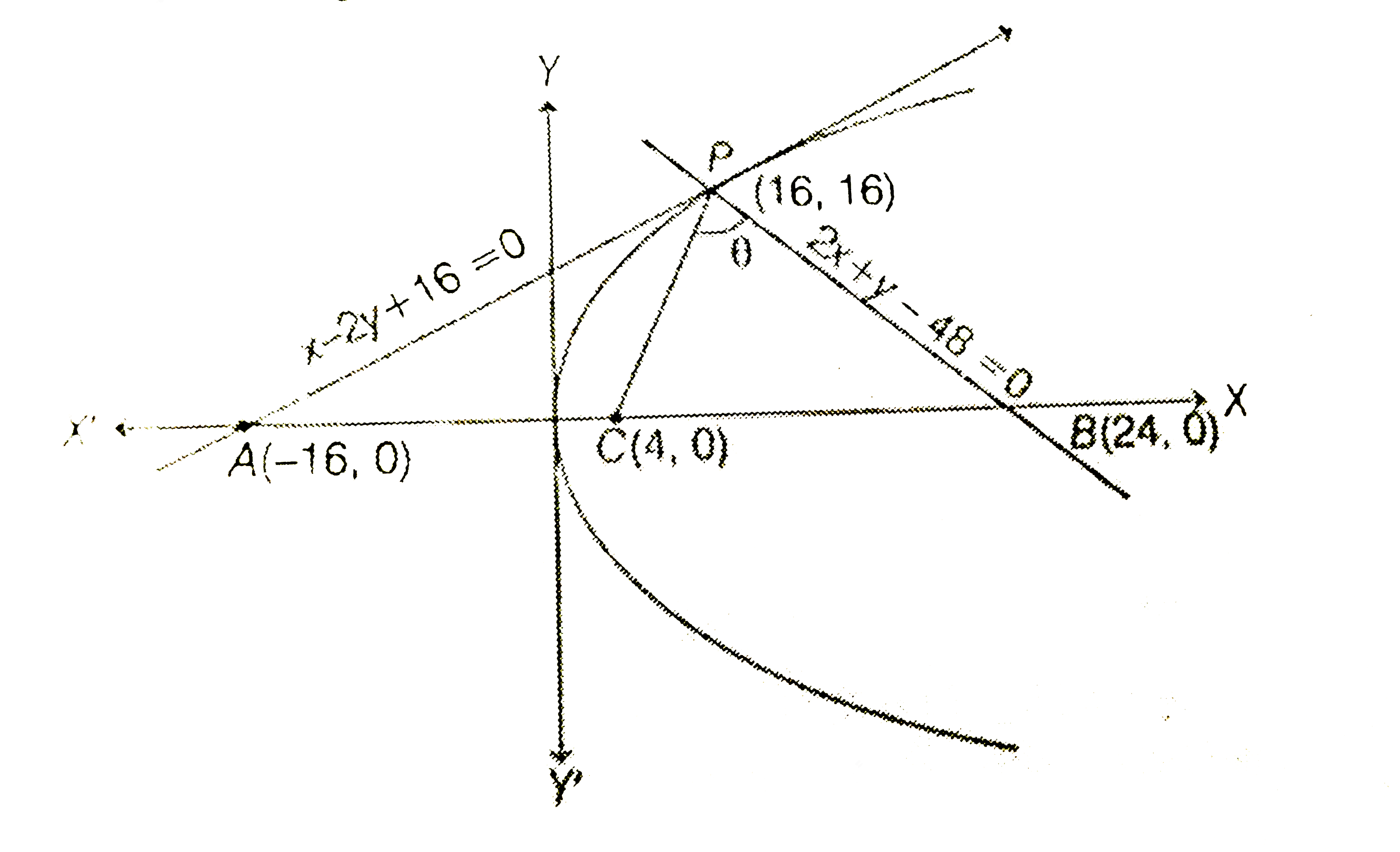
Tangent and normal are drawn at P(16,16) on the parabola y^2=16x which intersect the axis of the parabola at A and B respectively. If C is the centre of the circle through the points P,A and B and angle CPB=theta then the value of tan theta is

Tangent and normal are drawn at the point P-=(16 ,16) of the parabola y^2=16 x which cut the axis of the parabola at the points Aa n dB , rerspectively. If the center of the circle through P ,A ,a n dB is C , then the angle between P C and the axis of x is (a)tan^(-1)(1/2) (b) tan^(-1)2 (c)tan^(-1)(3/4) (d) tan^(-1)(4/3)

Normals are drawn at point P,Q,R lying on parabola y 2 =4x which intersect at (3,0) then area of △PQR is :-

Normals are drawn at points A, B, and C on the parabola y^2 = 4x which intersect at P. The locus of the point P if the slope of the line joining the feet of two of them is 2, is

The tangent and normal at P(t) , for all real positive t , to the parabola y^2= 4ax meet the axis of the parabola in T and G respectively, then the angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle passing through the points P, T and G is

The tangent PT and the normal PN to the parabola y^2=4ax at a point P on it meet its axis at points T and N, respectively. The locus of the centroid of the triangle PTN is a parabola whose:

Tangents are drawn to the parabola y^2=4a x at the point where the line l x+m y+n=0 meets this parabola. Find the point of intersection of these tangents.

Three normals are drawn from the point (7, 14) to the parabola x^2-8x-16 y=0 . Find the coordinates of the feet of the normals.

Suppose a parabola y = x^(2) - ax-1 intersects the coordinate axes at three points A,B and C, respectively. The circumcircle of DeltaABC intersects the y-axis again at the point D(0,t) . Then the value of t is

The equation of the tangent to the parabola y^(2)=16x inclined at 60^(@) to x axis is: