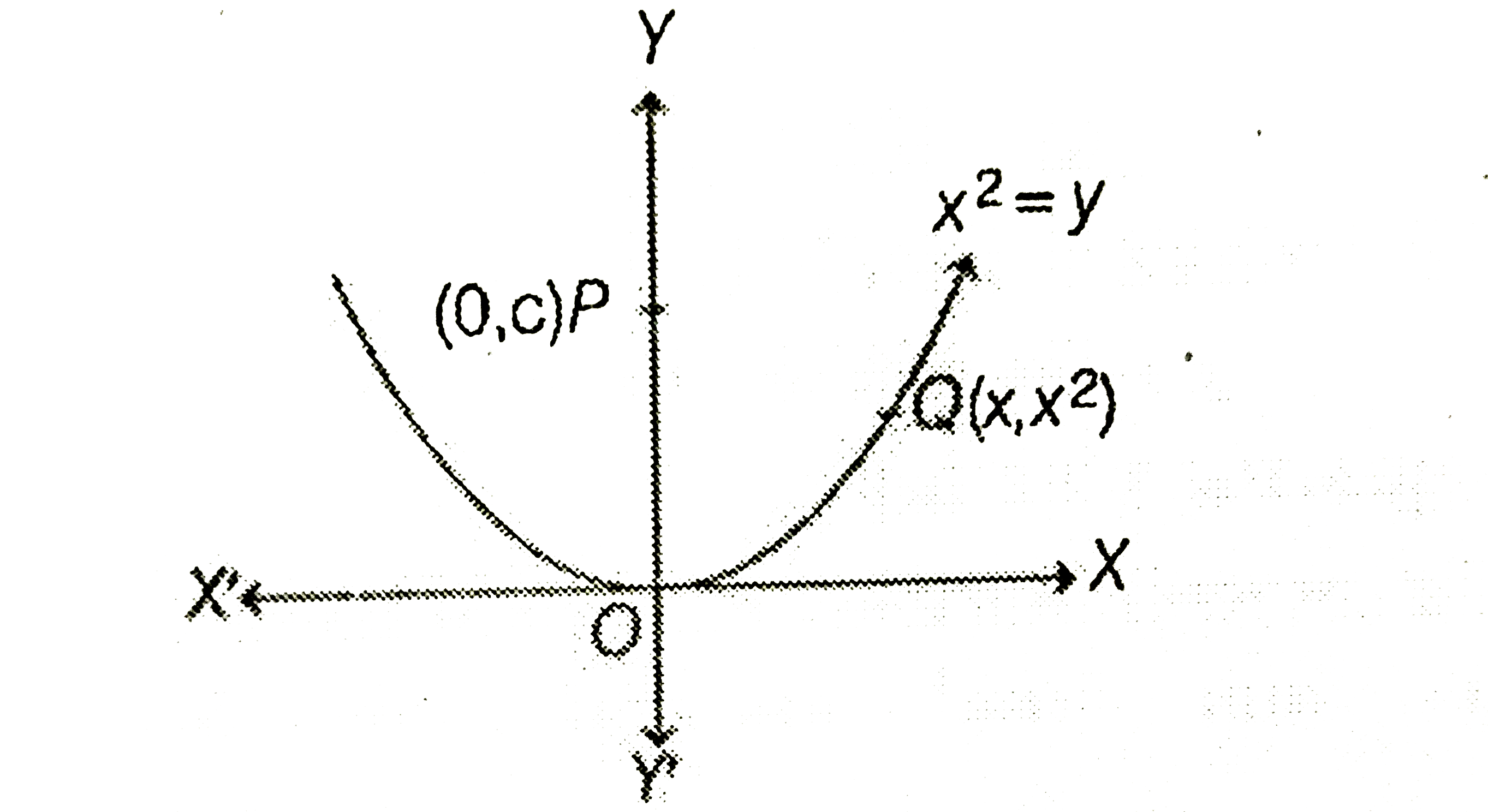Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the shortest distance of the point (0, c) from the parabola y=x^2...
Text Solution
|
- Find the shortest distance of the point (0, c) from the parabola y=x^...
Text Solution
|
- बिंदु (0 ,c ) से परवलय y=x^(2) की न्यूनतम दुरी ज्ञात कीजिए जहाँ 0lt ...
Text Solution
|
- परवलय y = x^(2) से बिंदु (0,a) कि न्यूनतम दूरी ज्ञात कीजिए।
Text Solution
|
- परवलय y=x^(2) से बिन्दु (0,c), जहाँ 0 le c le 5 की निम्नतम दूरी ज्ञात ...
Text Solution
|
- Find the shortest distance of the point (0, c) from the curve y=x^(2),...
Text Solution
|
- Find the shortest distance of the point (0, c) from the parabola y = x...
Text Solution
|
- Find the shortest distance of the point (0, c) from the parabola y = x...
Text Solution
|
- Find the shortest distance of the point (0, c) from the parabola y = x...
Text Solution
|