A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
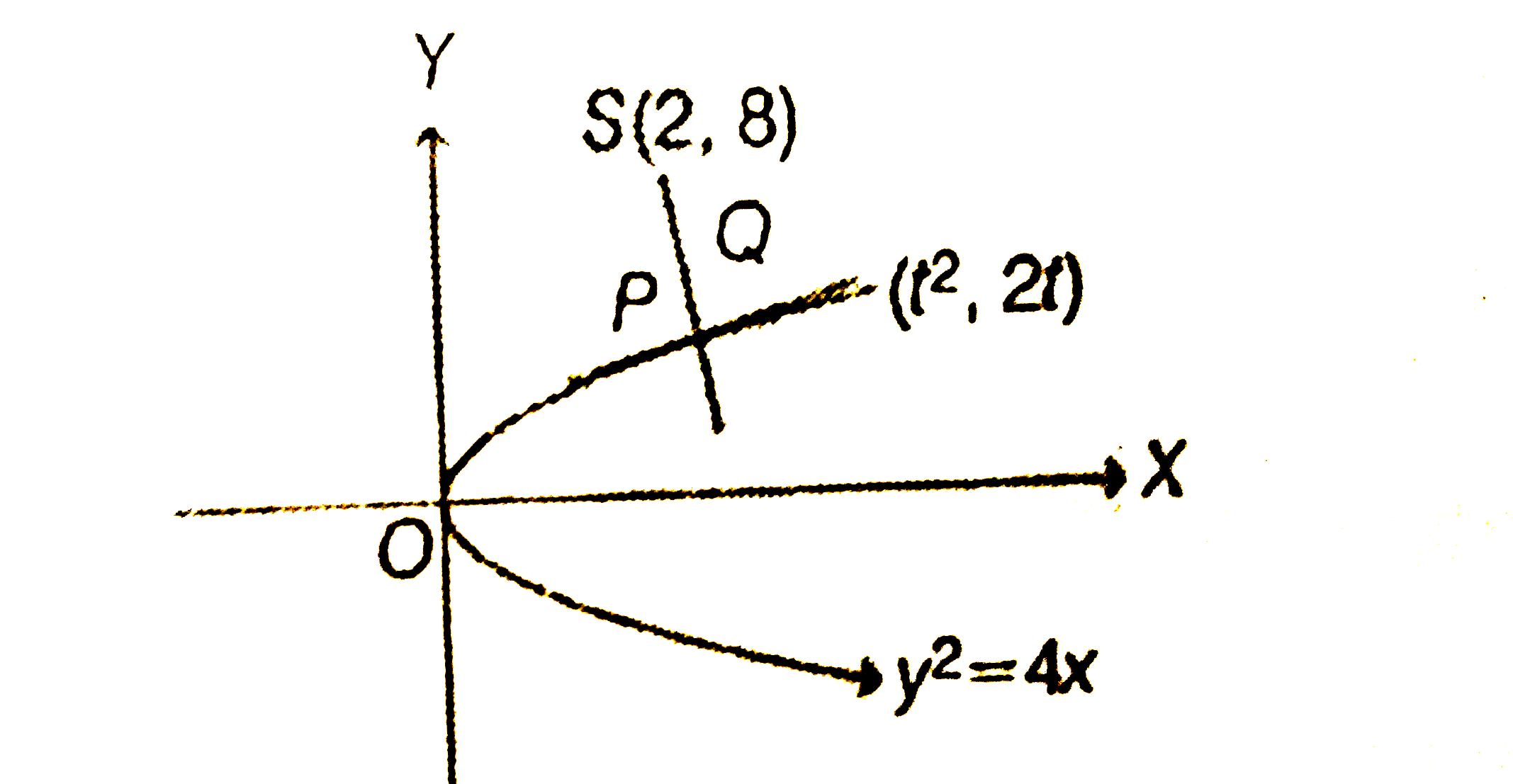
- Let P be the point on parabola y^2=4x which is at the shortest distanc...
Text Solution
|
- Let (x,y) be any point on the parabola y^(2)=4x. Let P be the point th...
Text Solution
|
- Let P be the point on parabola y^2=4x which is at the shortest distanc...
Text Solution
|
- Let (x, y) be any point on the parabola y^(2) = 4x . Let P be the poin...
Text Solution
|
- Let P be the point on the parabola y^(2) = 4x which is at the shortest...
Text Solution
|
- Let P be the point on the parabola y^(2)=4x which is at the shortest d...
Text Solution
|
- Let (x, y) be any point on the parabola y^2=4x . Let P be the point th...
Text Solution
|
- माना कि परवलय (parabola) y^(2)=4x पर P एक ऐसा बिन्दु है जो वृत्त x^(2)...
Text Solution
|
- Let (x,y) be any point on the parabola y^2 = 4x . Let P be the point t...
Text Solution
|