Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
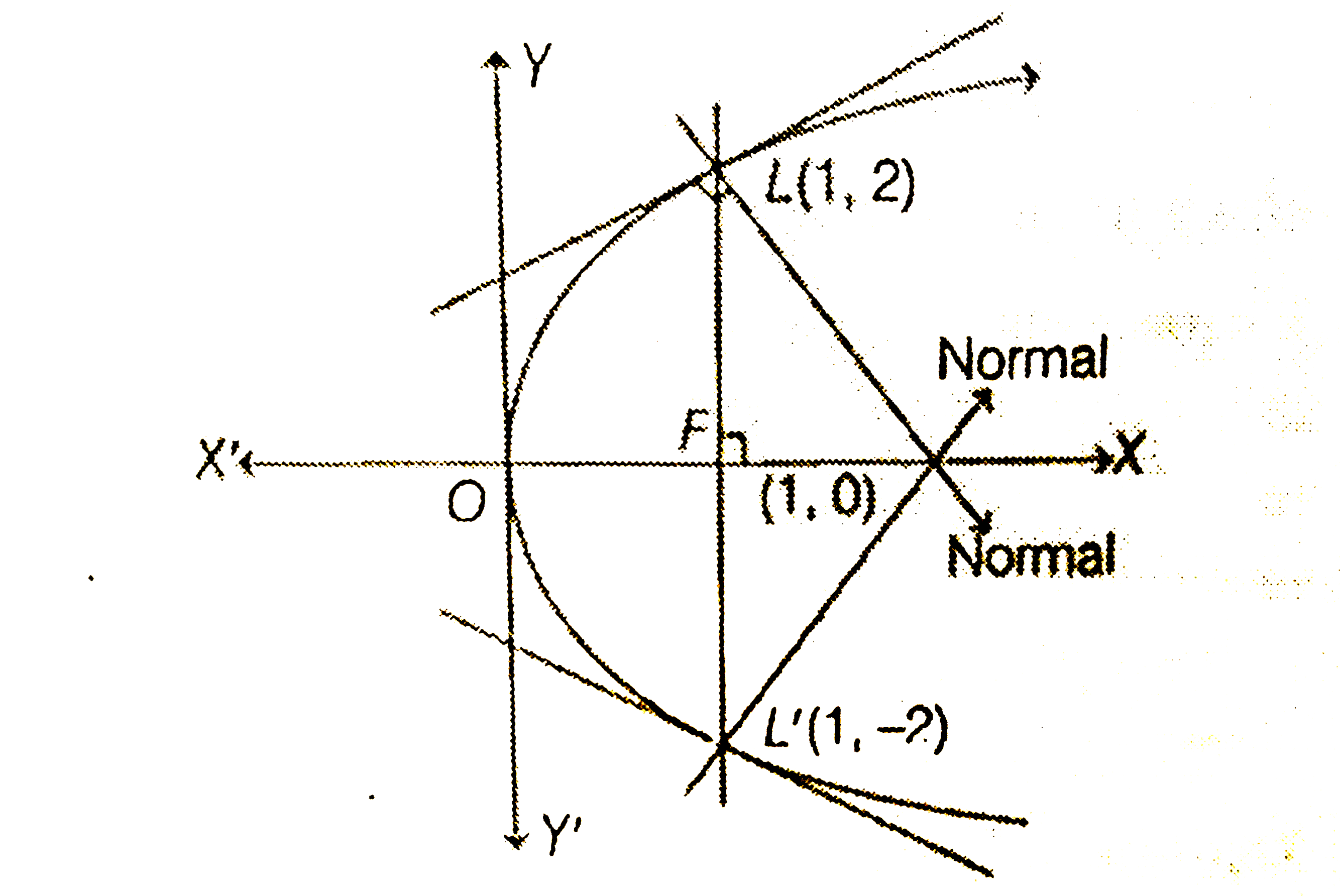
- If the normals of the paralbola y^2=4x drawn at the end points of its...
Text Solution
|
- The point of intersection of the tangents at the ends of the latus rec...
Text Solution
|
- ·If the normals of the parabola y^2=4x drawn at the end points of it...
Text Solution
|
- If the normals of the paralbola y^2=4x drawn at the end points of its...
Text Solution
|
- Circle is drawn with end points of latus rectum of the parabola y^2 = ...
Text Solution
|
- If the normals of the parabola y^(2)=4x drawn at the end points of its...
Text Solution
|
- If the normals of the parabola y^(2)=4x drawn at the end points of its...
Text Solution
|
- यदि परवलय (parabola) y^(2)=4x के नाभिलम्ब जीवा (latusrectum) के शिखर ब...
Text Solution
|
- y^2=4x என்ற பரவளையத்திற்கும் அதன் செவ்வகலத்திற்கும் இடையே பரப்பானது
Text Solution
|