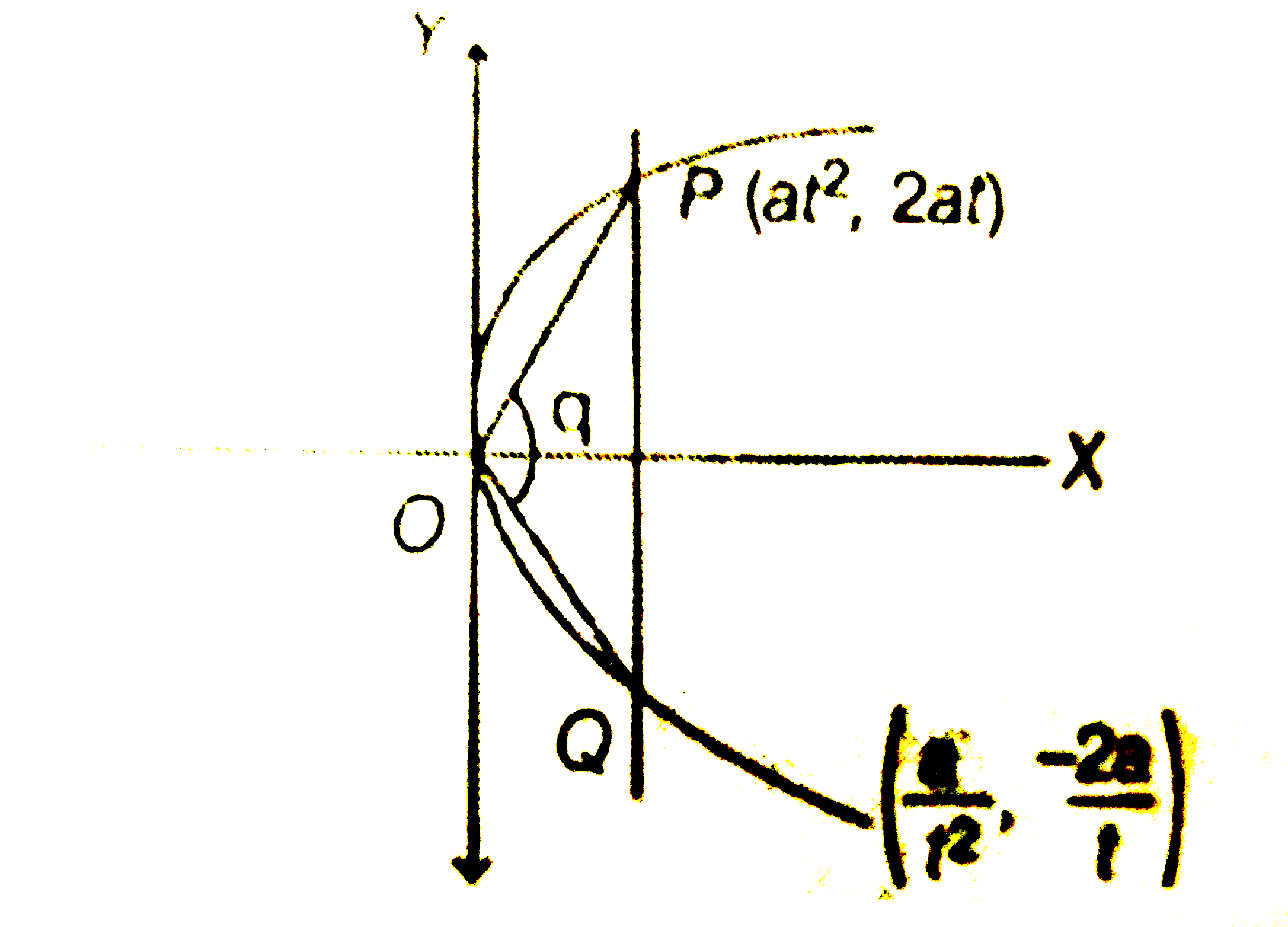A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- Let PQ be a focal chord of the parabola y^(2)=4ax. The tangents to the...
Text Solution
|
- Let PQ be a focal chord of the parabola y^(2)=4ax The tangents to the ...
Text Solution
|
- Let PQ be a focal chord of the parabola y^(2)=4ax . The tangents to th...
Text Solution
|
- Let PQ be a focal chord of the parabola y^(2)=4ax such that tangents a...
Text Solution
|
- Let PQ be a focal chord of the parabola y^(2) = 4ax . The tangents to ...
Text Solution
|
- Let PQ be a focal chord of the parabola y^(2) = 4ax . The tangents to ...
Text Solution
|
- Let PQ be a focal chord of the parabola y^2=4ax . The tangents to the ...
Text Solution
|
- माना कि PQ परवलय y^(2)=4ax की एक नाभीय जीवा है। बिन्दुओं P तथा Q पर पर...
Text Solution
|
- Let PQ be a focal chord of the parabola y^2 = 4ax The tangents to the ...
Text Solution
|