Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MBD-Lines and Angles-Exercise
- In fig. if a is greater than b by one third of right angle. Find th...
Text Solution
|
- If ray OC stands on line AB such that angleAOC = angleBOC (see fig. )...
Text Solution
|
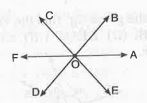
- In given fig. Rays OA, OB, OC, OD and OE have common initial point ...
Text Solution
|
- In the given Fig , lines, PQ and RS intersect each other at point O. ...
Text Solution
|
- In the given fig. , ray OS is on POQ. Rays OR and OT are the bisector...
Text Solution
|
- In fig. angleAOF and angleFOG form linear pair. angleEOB = angle FOC...
Text Solution
|
- Match the following : .
Text Solution
|
- In fig. angleAOF and angleFOG form linear pair. angleEOB = angle FOC...
Text Solution
|
- In fig. angleAOF and angleFOG form linear pair. angleEOB = angle FOC...
Text Solution
|
- In fig. angleAOF and angleFOG form linear pair. angleEOB = angle FOC...
Text Solution
|
- In fig. angleAOF and angleFOG form linear pair. angleEOB = angle FOC...
Text Solution
|
- In fig. angleAOF and angleFOG form linear pair. angleEOB = angle FOC...
Text Solution
|
- In given fig. AB and CD are two intersecting lines. OP and OQ are re...
Text Solution
|
- Angles forming a linear pair are supplementary.
Text Solution
|
- If two adjacent angles are equal, then each angle measures 90^@.
Text Solution
|
- Angles forming a linear pair can both the acute angles.
Text Solution
|
- Two distinct lines in a plane can have two points in common.
Text Solution
|
- If angles forming a linear pair are equal, then each of these angles i...
Text Solution
|
- If two lines intersect and if one pair of vertically opposite angles i...
Text Solution
|
- If two lines intersect and one of the angles so formed is a right angl...
Text Solution
|