Similar Questions
Explore conceptually related problems
MBD-Triangles-Exercise
- ABC is a triangle in which altitudes BE and CF to sides AC and AB are ...
Text Solution
|
- ABC is a triangle in which altitudes BE and CF to sides AC and AB are ...
Text Solution
|
- ABC and DBC are two isosceles triangles on the same base BC (See Fig. ...
Text Solution
|
- DeltaABC is an isoscelestriangle in which AB = AC. Side BA is produced...
Text Solution
|
- ABC is a right angled triangle in which angleA = 90^@ and AB = AC. Fin...
Text Solution
|
- Show that the angles of an equilateral triangle are 60^@ each.
Text Solution
|
- If vertical angle of an isosceles triangle is 40^@. Find the measure o...
Text Solution
|
- In given Fig. , AD = AE and D and E are points on BC, such that BD = ...
Text Solution
|
- If in given Fig. , PQ = PT and angleTPS = angleQPR, Prove that triang...
Text Solution
|
- Angles A, B and C of a triangle ABC are equal to each other. Prove tha...
Text Solution
|
- If the bisector of an angle of a triangle also bisects the opposite si...
Text Solution
|
- If the base of an isosceles triangle is produced both ways, show that ...
Text Solution
|
- If the bisector of the exterior vertical angle of a triangle be parral...
Text Solution
|
- ABCD is a square and DEC is an equilateral triangle. Prove that AE = B...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- AD is an altitude of an isosceles triangle ABC in which AB = AC. Show ...
Text Solution
|
- AD is an altitude of an isosceles triangle ABC in which AB = AC. Show ...
Text Solution
|
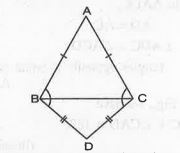 ). Show that `angleABD = angleACD`.
). Show that `angleABD = angleACD`.