Similar Questions
Explore conceptually related problems
MBD-Triangles-Exercise
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- AD is an altitude of an isosceles triangle ABC in which AB = AC. Show ...
Text Solution
|
- AD is an altitude of an isosceles triangle ABC in which AB = AC. Show ...
Text Solution
|
- Two sides AB and BC and median AM of one triangle ABC are respectively...
Text Solution
|
- Two sides AB and BC and median AM of one triangle ABC are respectively...
Text Solution
|
- BE and CF are two equal altitudes of a triangle ABC. Using RHS congrue...
Text Solution
|
- ABC is an isosceles triangle with AB = AC. Draw AP bot BC to show that...
Text Solution
|
- P is a point equidistant from two lines l and m intersecting at point ...
Text Solution
|
- The image of an object placed at a point before a plane mirror LM is s...
Text Solution
|
- Show that in a right angled triangle, the hypotenuse is the longest si...
Text Solution
|
- In Fig. , sides AB and AC of DeltaABC are extended to points P and Q ...
Text Solution
|
- In Fig. , angleB < angleA and angleC < angleD. Show that AD < BC.
Text Solution
|
- In DeltaABC, BC = 3.6 cm, CA = 2.8 cm. AB = 3.4 cm, arrange the angles...
Text Solution
|
- In DeltaABC if angleA = 48^@, angleB = 51^@, find the third angle and ...
Text Solution
|
- In DeltaABC if angleA = angleB=62frac(1^@) 2, find the third angle and...
Text Solution
|
- In the Fig. If AB = AD. Prove that AB > CD.
Text Solution
|
- ABC is an equilateral triangle. X is point on AC, Prove that BX > XC a...
Text Solution
|
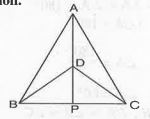 ).If AD is extended to intersect BC at P, show that AP bisects `angleA` as well as `angleD`.
).If AD is extended to intersect BC at P, show that AP bisects `angleA` as well as `angleD`.