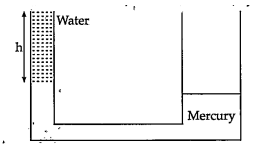
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two communicating vessels contain mercury. The diameter of one vessel ...
Text Solution
|
- A cylindrical vessel having diameter equal to its height is full of...
Text Solution
|
- Two communicating cylindrical tubes contain mercury. The diametr of on...
Text Solution
|
- Two communicating vessels contain mercury. The diameter of one vessel ...
Text Solution
|
- Mercury of density rho(m) is poured into cylinderical communicating ve...
Text Solution
|
- एक बेलनाकार बर्तन जिसकी ऊंचाई के बराबर व्यास होता है, पानी से भरा होता...
Text Solution
|
- A vessel contains mercury and water. An iron cylinder just floats vert...
Text Solution
|
- The diameter and height of a narrow cylindrical vessel are 10 cm and 1...
Text Solution
|
- In a U-tube of diameter 1.4 cm, 837 g mercury is poured. If the densit...
Text Solution
|