वे आकृतियाँ जिनके आकार समान होते हैं, परंतु माप आवश्यक रूप से समान नहीं हों, समरूप आकृतियाँ कहलाती हैं। हम समरूप आयतों को, उनकी विमाओं को एक ही अनुपात में बढ़ा अथवा घटा करके बना सकते हैं। आइए समरूप आयतों को वर्गाकार टाइलों का उपयोग करके बनाएँ।
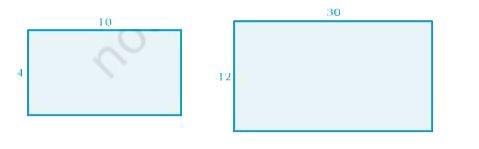
एक समरूप आयत की लंबाई क्या होगी यदि उसकी चौड़ाई 12 टाइलों से बनायी गयी है? आइए एक ऐसे आयत को लें, जिसकी लंबाई के अनुदिश 10 वर्गाकार टाइलें हैं और चौड़ाई के अनुदिश 4 वर्गाकार टाइलें हैं, जैसा आकृति में दर्शाया गया है।

`10xx4` आयत बनाने के लिए टाइलों का प्रयोग कीजिए।
आयत की चौड़ाई 12 टाइल बढ़ाने के लिए इसमें टाइलें जोड़िए या लगाइए। नये आयत की चौड़ाई प्रारंभिक आयत की चौड़ाई की तिगुनी है। दोनों आयतों की लंबाइयों को समानुपात में रखने के लिए, इस नये आयत की लंबाई भी प्रारंभिक आयत की लंबाई की तिगुनी होनी चाहिए।

आयत की लंबाई 30 टाइलें करने के लिए, इसमें टाइलें जोड़िए।
अपने उत्तर की जाँच करने के लिए, हम सीधे समानुपात की अवधारणा का उपयोग कर सकते है।
`(4)/(10)=(12)/(30)`
या `(2)/(5)=(2)/(5)`
स्वयं कीजिए
वर्गाकार टाइलों का प्रयोग करते हुए दी हुई विमाओं के समरूप आयत बनाइए तथा लंबाई x का मान ज्ञात कीजिए।
(a) प्रारंभिक आयत की चौड़ाई 8 टाइल हैं और लंबाई 6 टाइल हैं। समरूप आयत 16 टाइल चौड़ा है और x टाइल लंबा है।
(b) प्रारंभिक आयत 3 टाइल चौड़ा और 7 टाइल लंबा है। समरूप आयत 9 टाइल चौड़ा है और x टाइल लंबा है।


