Text Solution
Verified by Experts
Topper's Solved these Questions
THE SOLID STATE
ARIHANT PUBLICATION|Exercise PART II (QUESTION FOR PRACTICE) (Long Answer Type Questions)|2 VideosTHE SOLID STATE
ARIHANT PUBLICATION|Exercise PART II (QUESTION FOR ASSESSMENT) (Multiple Choice Type Questions)|3 VideosTHE SOLID STATE
ARIHANT PUBLICATION|Exercise PART II (QUESTION FOR PRACTICE) (Short Answer Type I Questions)|14 VideosSURFACE CHEMISTRY
ARIHANT PUBLICATION|Exercise CHAPTER PRACTICE ( LONG ANSWER TYPE QUESTIONS)|1 Videos
Similar Questions
Explore conceptually related problems
ARIHANT PUBLICATION-THE SOLID STATE -PART II (QUESTION FOR PRACTICE) (Short Answer Type II Questions)
- How many lattice points are there in one unit of each of the following...
Text Solution
|
- How will you distinguish between the following pairs of terms? Cryst...
Text Solution
|
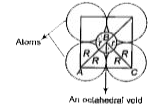
- If the radius of the octahedral void is r and radius of the atoms in c...
Text Solution
|
- An element crystallises in fcc lattice having edge length 400 pm, Calc...
Text Solution
|
- An element with molar mass 27 g "mol"^(-1) forms a cubic unit cell wi...
Text Solution
|
- An element with molar mass 2.7xx10^(-2) "kg mol"^(-1) forms a cubic u...
Text Solution
|
- An element occurs in bcc structure. It has a cell edge length of 250 p...
Text Solution
|
- Niobium crystallises in a body-centred cubic structure. If its density...
Text Solution
|
- Aluminium crystallises in a cubic closed packed structure. Its metalli...
Text Solution
|